上一节，简单的介绍了计算机时如何将三维世界中的点转化成屏幕上的二维点坐标的，知道了透视矩阵的作用。这一节内容，就是介绍其中的数学计算的过程。
在三维计算机图形学中，那些呈现在屏幕（画布canvas）上的每个点，都是由三维的点转化的，它们组成了屏幕上的图像。在前面的文章中，我介绍了透视矩阵，透视矩阵的作用就是将三维的点转化成二维的点，展现在屏幕上，也给大家讲解了透视投影矩阵的计算，所以本节内容 当然并不是再次计算透视投影矩阵，而是更精细化的一步一步的将三维点转化到二维点的的计算过程展现给大家。
首先要说明的是，将三维点转化成二维点的方法有很多，透视矩阵仅是无数方法中的一种，比如我在之前文章介绍的平行投影矩阵（正射投影矩阵），它也可以将三维点转化成二维点，只是与透视投影转化的结果稍有不同。所以将三维点转化成二维点，并没有限制转化的结果完全一样，既然结果不一样，那么转化法自然有无穷多种，而且即使结果一致，转化方法一般也会有多种，就像解数学题一样，通常会有多种解法。
我接下来要讲解的过程，是模拟透视投影矩阵的，透视投影矩阵转化后的图像与人眼观察的图像类似（简单的说就是近大远小）。
关于坐标系的概念，可以看这篇文章，这里我们再重新回顾下。
无论是在图形软件中还是编程中，为了高效工作，一般都会有世界坐标系（world coordinates）和局部坐标系（local coordinates）,世界坐标系是相对于世界空间的（world space），所有的物体（object）都处于这个世界空间中，它们在世界空间中都有一个位置（世界坐标），但是它们也有自己所处的一个独立的空间，即局部空间。以软件建模为例，当设计师在设计房子中的一个桌子时，它会单独先设计这个桌子，假设桌子底部中心原点(0, 0, 0)，那么桌子顶部中心的坐标为(0, 1.2, 0)，这里说的坐标其实就是局部坐标系中的坐标，当建模完成后，设计师将桌子移动到房子场景（世界坐标）中的某个位置，桌子在房子场景中的某个位置即桌子的世界坐标。可能在使用软件时，设计师并没有意识到世界坐标与局部坐标这两个概念。
此时，你可能还没有理解为什么会区分世界坐标系和局部坐标系，不知道为什么要搞这么复杂，如果在定义场景中的所有物体时，都用世界坐标系不好吗，好像还简化了。
事实其实不是你想的那样。以我们现在所处的地球为例，都知道经纬线吧，经纬线也是一个坐标，地球上每个物体都有一个确定的经纬线位置，你可以将它看成世界坐标，但是你在平时的日常交流中，会用经纬线来确定位置吗？别人向你问路时，“您好，请问东方明珠怎么走？”，“往前左转，然后右转，直走就是了。”，你肯定不会这样回答“东方明珠在东经121.506377，北纬31.245105”。所以世界坐标并不是在所有情况下，都适用的，所以才会有各种各样的坐标系存在。
三维变换矩阵是一个4X4的矩阵，关于为什么是4x4的而不是3x3的矩阵，以及平移、旋转、缩放矩阵的证明可以看这篇文章。
三维场景中所有的线性变换，都是由平移、旋转和缩放组成。
4x4的矩阵（列为主）的前三列表示的是，旋转后i帽、j帽、z帽 的坐标，即线性变换矩阵的每一列表示的都是变换后的坐标系的x、y、z轴的单位向量的表示。
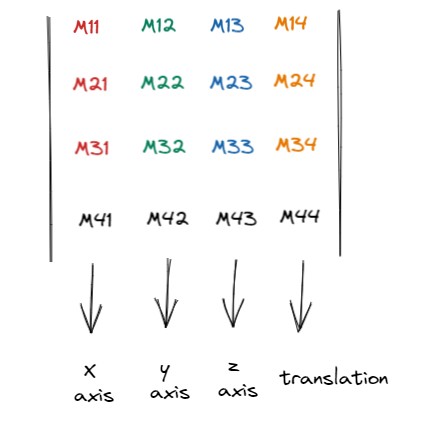
上图中(M11,M21,M31)表示的是旋转后的i帽，(M12, M22, M32)是j帽，(M13, M23, M33)是z帽，至于为什么可以看这篇文章。
假设有如下场景，点在世界坐标系中的坐标为(-0.31, 1.44, -2.49)，在局部坐标系中的坐标为(-0.5, 0.5, -0.5)。
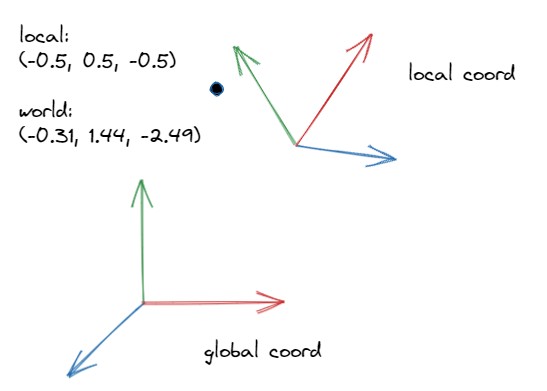
那么肯定存在一个矩阵Matrix_WorldToLocal，可以将它在世界坐标系中的坐标转化成局部坐标系中的坐标，也存在一个Matrix_LocalToWorld可以做逆向转换，将局部坐标转化成世界坐标。且这两个矩阵互为逆矩阵。
Lcoord = Matrix_WorldToLocal * WCoord
Wccor = Matrix_LocalToWorld * LCoord
Matrix_LocalToWorld = Matrix_WorldToLocal^-1 // 逆矩阵
在游戏世界中，不同玩家看到的场景是不一样的，假设以玩家为中心，建立一个坐标系，那么每个玩家所代表的坐标系就是不同的局部坐标系。
一般在CG中称这个坐标系为摄像机坐标系，也可以称视觉坐标系，此时这个局部空间，被称为摄像机空间或者视觉空间。
所以计算机图形学中的经常提到的相机的作用，仅是将世界场景转化为摄像机场景，即世界坐标系转化为摄像机坐标系，而用作转化的矩阵，通常被称之为视觉矩阵。
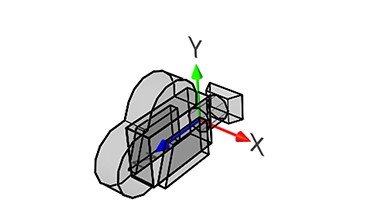
注意，在摄像机空间中，摄像机为原点，视线方向为负z轴，也就是所有z坐标大于0的物体将不会出现在摄像机的视野中。
介绍了那么多，下面我们计算如何将点从世界坐标系的点转化成二维点。
首先将点从世界坐标系转化到摄像机坐标系中，这个可以通过矩阵完成。
P_camera = P_world * Matrix_worldToCamera
然后将P_camear投射成二维坐标。
这一部分的过程在矩阵证明的第三篇文章中有，这里再介绍下。
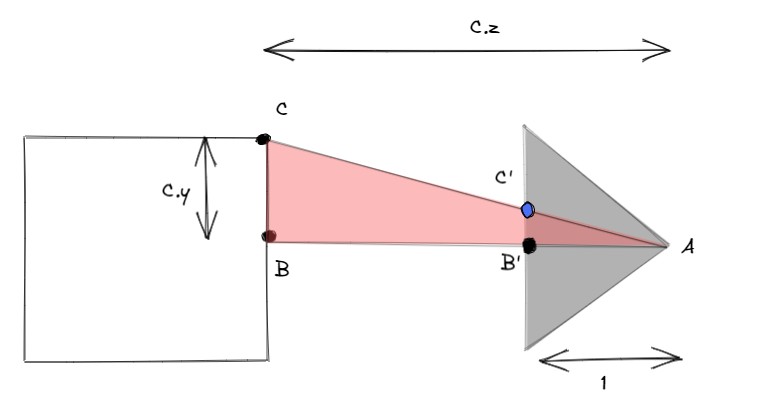
相机在坐标系的原点，看向坐标轴的负z轴（在图形学中这是一个惯例，摄像机在摄像机坐标系的原点，看向z轴负方向），假设有一个点C投影在画布上为C'，从X轴看向yz平面，此时场景如上图所示。假设此时画布离原点距离为1，此时AB长度为C.z，BC长度为C.y，根据相似三角形计算得到：
C.y / C.z = C'.y / 1
C'.y = C.y / C.z
同理可得：
C'.x = C.x / C.z
即，假设摄像机空间中有一点Pcamera，那么投射到二维画布中的P'的坐标为：
P'.x = Pcamera.x / Pcamera.z
P'.y = Pcamera.y / Pcamera.z
注意在摄像机坐标系中，摄像机能看到的物体都是摄像机坐标系的负z轴，因为摄像机只能看到z为负值的点，所以经过变换后x和y的坐标也变符号了，这显然不是我们想要的结果，因为会出现上下颠倒的结果，我们只需要将等式中的Pcamera.z改成-Pcamera.z即可。
P'.x = Pcamera.x / (-Pcamera.z)
P'.y = Pcamera.y / (-Pcamera.z)
所以，一般将世界坐标系中的点转化为二维点，要做两件事：
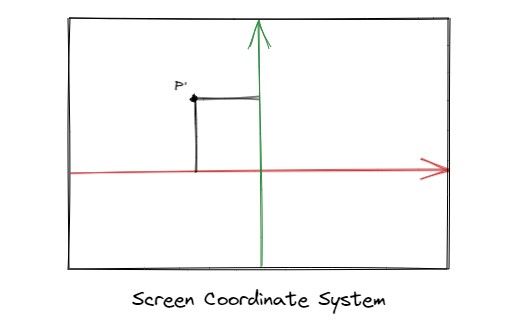
目前为止，我们得到了一个点P'，它实际上是一个落在画布上的二维点，所以此时可以忽略它的z坐标，而这些二维点所落在的画布空间被称为屏幕空间（screen space）或者图像平面（image plane），所处的坐标系统被称为屏幕（图像）坐标系统（scrren or image coordinate system），屏幕空间是一个无限大的平面，但是图像却是有固定尺寸的，所以会进行一个裁剪过程，在原点附近裁剪一个矩形区域，矩形区域内的图像才会被绘制。裁剪后的坐标系如下图所示，如果点P'在裁剪的区域内，那么它可以被看到，否则看不到。
接下来我们需要将其转换到**标准设备坐标系（NDC）**中，在坐标系统文章中我们说过NDC的范围是-1~+1。
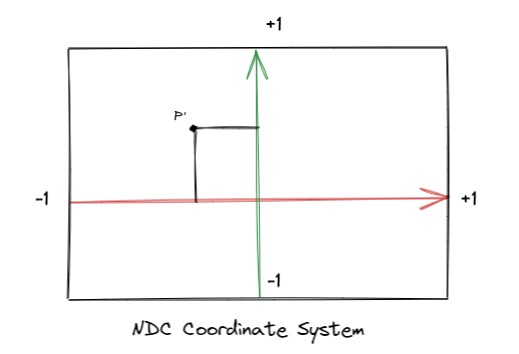
假设裁剪后的屏幕坐标系宽度width和高度height，可以计算出点在ndc中的坐标。
Pn'.x = 2 * P'.x / width;
Pn'.y = 2 * P'.y / height;
最后一步也很简单，计算机需要将NDC中的坐标转换成**栅格坐标系统（raster coordinate system）**中的坐标。
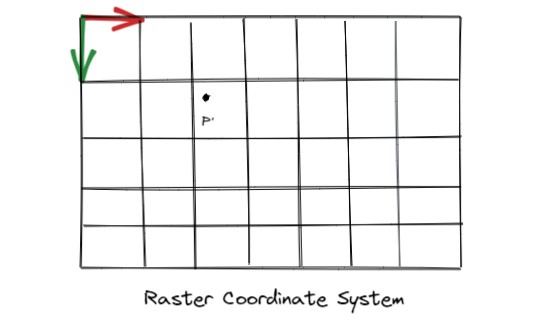
在栅格坐标系中，单位是像素（pixel），其原点在屏幕的左上角，y轴正方向朝下，x轴正方向朝左，我们知道了要展示的屏幕的像素宽度PixelWidth和高度PixelHeight，所以我们的目的就是在x方向上做[-1, +1]至[0, PixelWidth]的转换，在y方向上做[+1, -1]至[0, PixelHeight]的转换，注意y方向与x方向的区别。
P'r.x = (Pn'.x + 1) * PixelWidth / 2;
P'r.y = (1 - Pn'.y) * PixelHeight / 2;
现在，我们已经完全将一个三维点，转化成屏幕上的二维像素点了。通常在二维canvas绘图时，通常说的屏幕坐标就是栅格坐标系统。
最后，总结一下整个过程：
（完）