3D图形学中的矩阵变换(三) #
本篇文章是我翻译的一篇文章,原文地址:OpenGL Projection Matrix。 文章介绍了正射(平行)投影矩阵和透视投影矩阵的证明方法,作者讲述的很好,我看完之后觉得很有帮助,所以直接翻译了,希望更多的人能看到这篇文章。
概述 #
计算机显示器是一个2D平面。OpenGL渲染时必须将一个3D的场景投影在屏幕上成为一个2D的图片。GL_PROJECTION矩阵的就是用作这种投影变换。首先,其将所有的顶点数据从视觉坐标系(眼坐标系)转化到裁剪空间。然后,通过除以裁剪坐标系中的w分量,将转化后的裁剪坐标变换成标准设备坐标系(NDC)。
因此,我们必须记住GL_PROJECTION集成了裁剪和转化成标准设备坐标系的功能。下面的模块讲述了,如何从以下6个参数建立投影矩阵:left、right、bottom、top、near和far等边界值。
需要注意的是,裁剪空间中的平头截体的裁剪过程发生在,除以wc分量之前。将裁剪坐标 xc, yc和zc和wc进行比较,如果其中任意一个值小于wc或者大于wc,那么这个顶点将会被裁剪掉,渲染时会丢弃这个顶点。
-wc < xc,yc,zc < wc
当裁剪发生时,OpenGL会重新构建裁剪的边界和边线。
透视投影 #
在透视投影时,裁剪截体是一个锥形的,然后被映射到标准设备坐标系中(一个立方体),NDC的x、y和z轴的范围都是从-1至+1。
注意,视觉坐标系是右手坐标系,而NDC使用的是左手坐标系,它们的z值方向是相反的,在视觉坐标系中,摄像机在原点,观察方向为z轴的负值方向,但是在NDC中,摄像机的观察方向却是z轴的正值方向。因此,glFrustum()的near和far参数必须大于0,所以在构建GL_PROJECTION矩阵时,我们必须对它们取反。
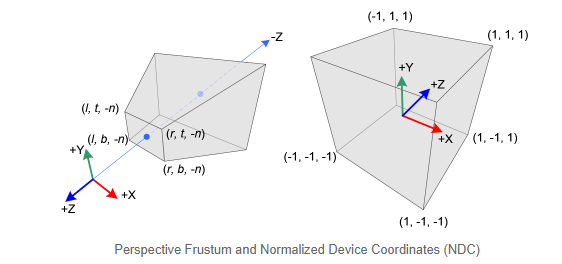
在openGL中,视觉空间中一个3D的点会被投影在近平面上(投影面)。下面的示意图展示了视觉坐标系中的点(xe, ye, ze)是如何投影到近平面上的(xp, yp, zp)的。
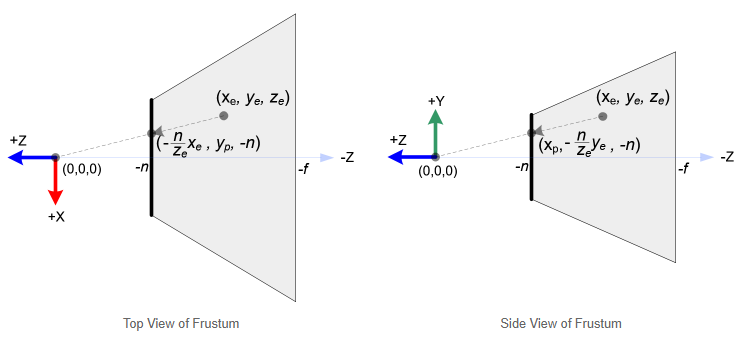
从上向下看向锥形截体,视觉坐标系的x坐标,xe会被映射到xp,可以通过相似三角形比例特性计算出xp:
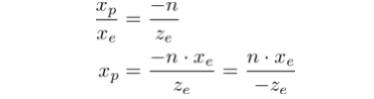
从侧面看向锥形截体,可以通过同样的方法,计算出yp:
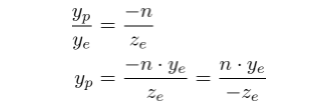
可以看到,xp和yp都依赖于ze,并且和-ze成反比的关系。换句话说,它们都被-ze除。这是构建GL_PROJECTION矩阵的第一个线索。当视觉坐标系的坐标通过乘以GL_PROJECTION矩阵转化成裁剪坐标,转化后的裁剪坐标任然是一个齐次坐标。最后通过除以w分量,转化成标准设备坐标系(NDC)。(可以在OpenGL变换中了解更多细节。)
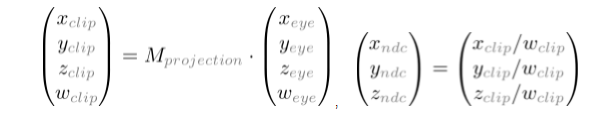
因此,我们可以将裁剪坐标的第四个分量设置为-ze. 因此GL_PROJECTION矩阵的第四行变成了(0, 0, -1, 0).
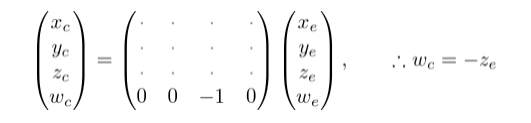
接下来,我们将xp和yp映射到标准设备坐标系中的xn和yn, 可以使用如下线性关系进行映射:[l, r] => [-1, 1] 和[b, t] => [-1, 1]。

然后,我们把上面等式中的xp和yp替换掉。

注意,上面的等式中,最后都转化为除以-ze,这正好与透视除法(xc/wc, yc/ wc)对应。在此之前,我们已经将wc设置为-ze了,因此等式括号中的部分,变成了xc和yc。
通过这些等式,我们可以得出GL_PROJECTION矩阵的第一行和第二行。
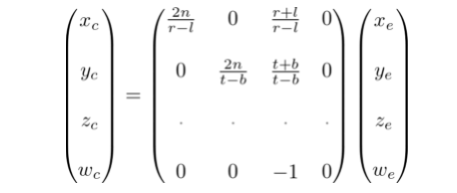
现在,我们只需要再计算GL_PROJECTION矩阵的第三行了。计算zn和计算xn、yn有点不同,因为视觉坐标系中的ze总是被投影到近平面(-n)上。但是我们需要一个独特的z值进行裁剪和深度测试。而且,我们还能够对其逆投影(逆转换)。因为z与x和y无关,我们可以借助w分量来寻找zn和ze的关系。因此我们可以指定GL_PROJECTION矩阵的第三行如下:
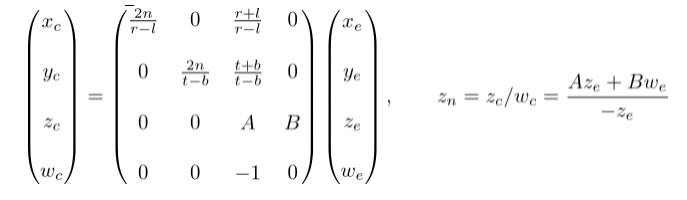
在视觉坐标系中we等于1,所以等式变成了:
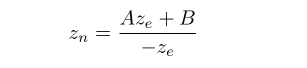
为了计算出系数A和B, 可以利用(ze, zn)的关系;(-n, -1)和(-f, 1), 将他们放进上面的等式中:
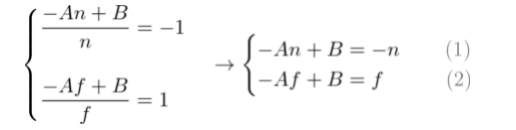
计算出A和B的值:
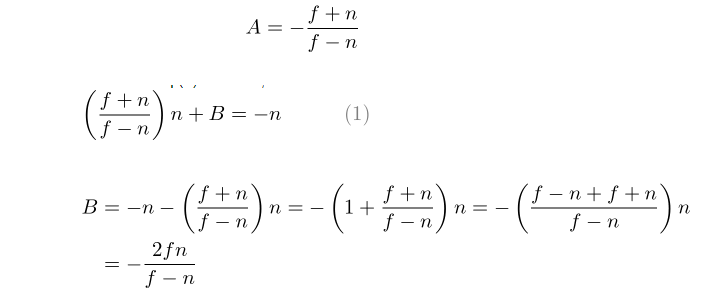
我们得到了A和B的值,所以ze和zn的关系变成:
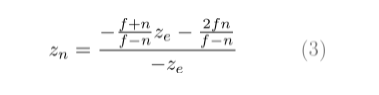
最后我们得到了完整的GL_PROJECTION矩阵:
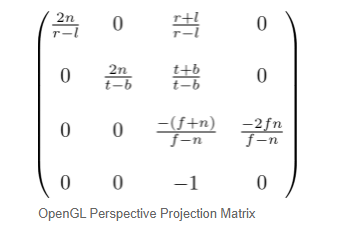
上面的投影矩阵是一个通用锥形截体的矩阵,如果视觉空间是对称的,满足r=-l并且t=-b,我们可以将上面的矩阵简化如下:
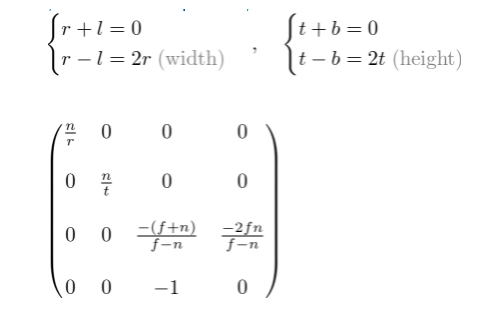
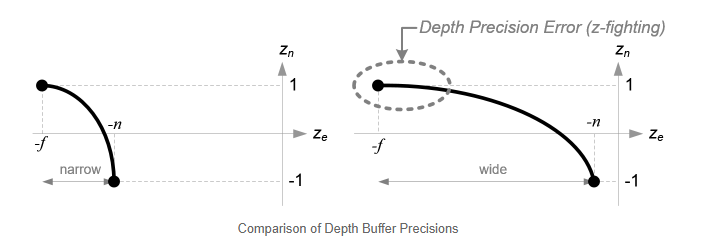
在讨论正射投影之前,我们在重新看一下ze和zn的关系。通过等式3,你注意到这是一个关系函数,但是ze和zn并不是线性关系。这意味着,离近平面越近精度越高,离近平面越远精度越低。如果[-n, -f]的范围越大,它会导致精度问题(z-fighting);在远平面附近的点的ze值发生很小的变化并不会影响zn的值。所以n和f的差值尽量小,这样可以减少深度缓冲的精度问题。
正射投影 #
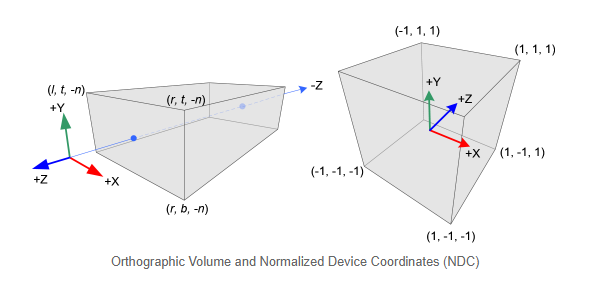
正射投影矩阵的建立比透视投影矩阵的建立会简单很多。
视觉空间坐标系中的xe,ye和ze分量,都会被线性的映射到标准设备坐标系(NDC)中。仅需要缩放视觉空间到标准设备空间(范围是-1~+1)中,然后将其移动到原点位置。接下来通过线性关系,计算GL_PROJECTION正射投影矩阵的各个值。

因为正射投影不需要w分量,所以矩阵的第四行仍然为(0, 0, 0, 1)。因此完整的GL_PROJECTION正射投影矩阵如下:

如果截体区域是对称的r=-l并且t=-b, 矩阵可以简化如下:
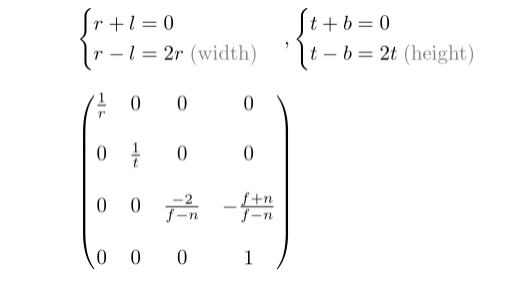
(完)