欧拉角 #

方位 #

在讨论欧拉角前，我想阐明一个概念：方位（orientation）。方位与方向（direction）不同，可以用向量描述方向，但是不能用一个向量描述一个方位，当将一个向量绕轴自转时，向量不会有任何变化。

然而当一个物体朝向一个特定的方向，让其按照向量一样自转时，物体的方位发生了变化。

描述一个物体的方位时，通常是相对于一个已知方位的旋转描述的，旋转的量称为角位移。所以描述方位等价于描述角位移。

描述方位有三种方式：

• 矩阵
• 欧拉角
• 四元数

本篇文章介绍欧拉角。

基本思想 #

欧拉角的基本思想是将角位移分解为绕三个互相垂直轴的三个旋转组成的序列。其实任意三个轴和任意顺序都是可以的，一般使用笛卡尔坐标系的三个轴，并按照一定顺序所组成的旋转序列。这里介绍最常用的 ”heading-pitch-bank" 系统。

最初让物体开始于"标准方位"——物体局部坐标系与世界坐标系的轴重合。然后依次做 heading 旋转，然后做 pitch 旋转，最后做 bank 旋转。

• heading 旋转：绕 y 轴旋转一定角度，因为最开始位于标准方位，所以 y 轴即是世界坐标系轴，也是物体局部坐标系轴。
• pitch 旋转：绕物体局部坐标系的 x 轴旋转一定角度。
• bank 旋转：绕物体局部坐标系的 z 轴旋转一定角度。

下面依次是原始方位，做 heading-pitch-bank 旋转的示意图。

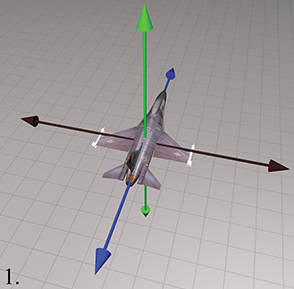
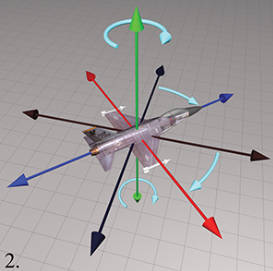
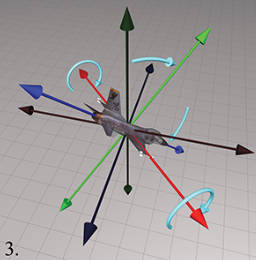
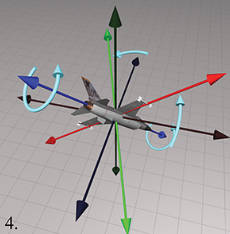
其他约定 #

• heading-pitch-bank: 也有其他系统名称，例如 roll-pitch-yaw，其中 roll 等价于 bank，yaw 等价于 heading。他的顺序和 heading-pitch-bank 顺序相反，它定义了向量从物体坐标系到世界坐标系的旋转顺序。
• 任意三个轴都能作为旋转轴，不一定使用笛卡尔坐标系轴，但是笛卡尔轴比较有意义。
• 旋转的正方向可以是左手法则也可以遵循右手法则，按照一定规则定义即可。
• 旋转可以以不同顺序进行，顺序并不重要。

只要理解其原理即可。

优点 #

• 简单易于使用。
• 与矩阵相比，占用内存小，只需要三个数字即可。

缺点 #

主要的缺点有两个：

• 给定方位的表达式不唯一。
• 两个角度间求插值非常麻烦。

这里仅讨论第一个缺点。将一个角度加上 360 度的倍数，显然不会改变方位。另外 pitch 135 度等价于 heading 180 度，pitch 45 度，然后 bank 180 度。

为了保证任意方位都只是独一无二的，必须限制角度的范围。一种技术是将 heading 和 bank 限制在 $[-180^\circ, +180^\circ]$ 之间，pitch 限制在 $[-90^\circ, +90^\circ]$ 之间。

还有一个著名的问题是万向锁（Gimbal Lock），举个例子，先 heading $45^\circ$ 再 pitch $90^\circ$，与先 pitch $90^\circ$ 再 bank $45^\circ$ 是一样的。原因是一旦选择 $\pm90^\circ$ 为 pitch 角，第一次和第三次旋转的旋转轴就都是竖直轴了，等价于损失了一个自由度，这种现象被称为万向锁。

（完）