本文以三维笛卡尔坐标系为例，讲述如何用矩阵表示坐标系、点以及向量。为了方便描述用 p(a,b,c) 表示点，用 v(a,b,c) 表示向量。
假设现有如下坐标系，原点坐标为 p(0,0,0)，x 轴的方向为 v(1,0,0)，y 轴方向为 v(0,1,0)，z 轴方向为 v(0,0,1)，这三个方向向量是坐标系的三个基向量 i、j、k。
在图形学中会大量用到矩阵的运算，所以无论是点、向量以及坐标系我们都需要用矩阵去表示它们。
线性空间中，向量集中任意一个向量可以通过基向量描述。例如向量 v1 v(a, b, c)：
v1 = a * i + b * j + c * k; // i, j, k 为 x，y，z 轴方向的基向量
// 加上一个零向量
v1 = a * i + b * j + c * k + 0 * o; // o 表示零向量
用矩阵表示上述公式：
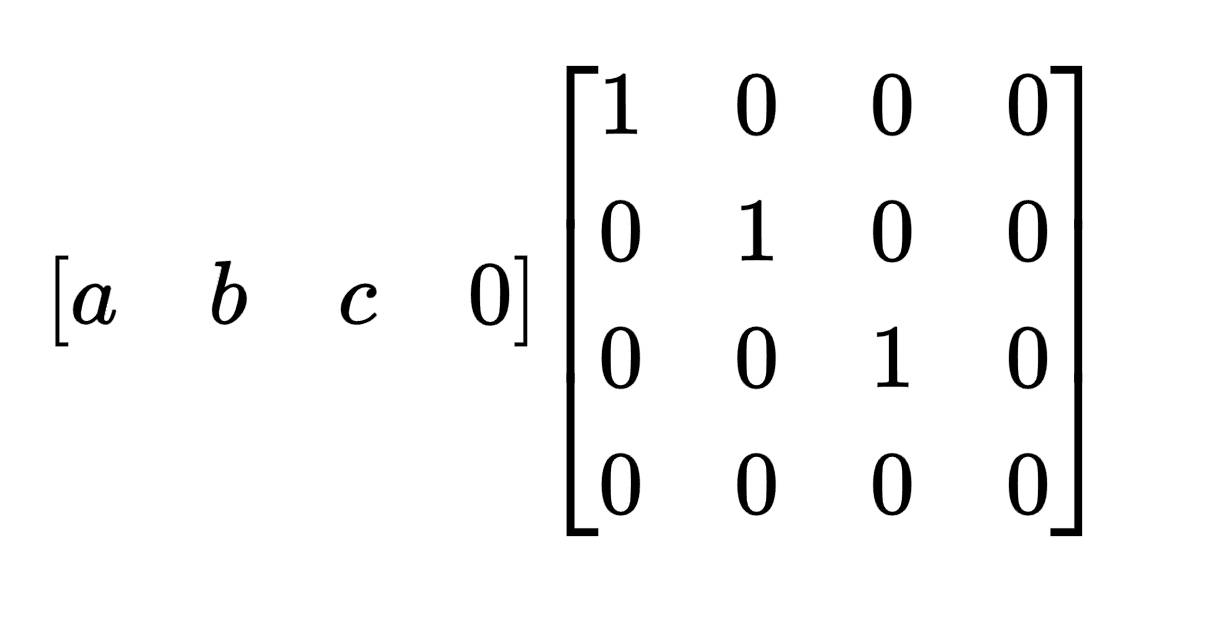
上述等式的左边即为向量的矩阵表示：向量表示为前面 n 个元素为坐标系的系数，最后一个元素为 0 的行矩阵（也可以表示为列矩阵）
点可以表示为一个点向某个方向移动，例如这个方向为 d。例如点 p1 p(a, b, c) 表示为：
p1 = 1 * o + a * d.x + b * d.y + c * d.z; // o 表示坐标系原点，d 表示移动向量
用矩阵表示上述公式：
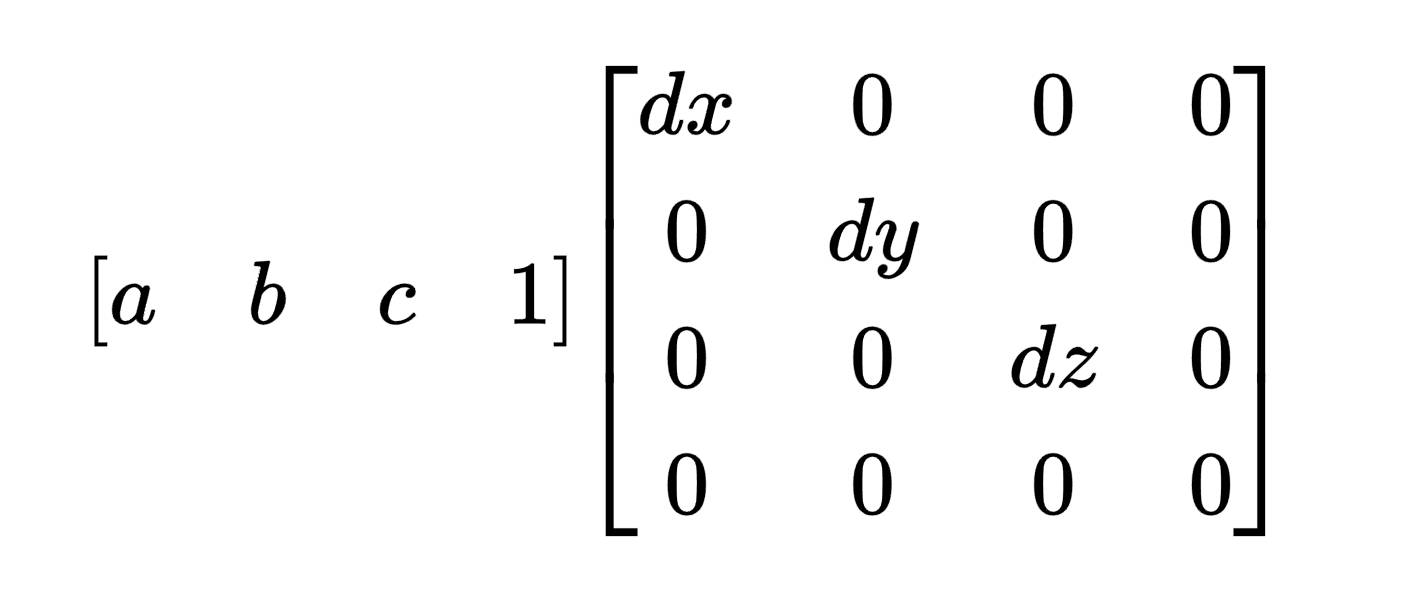
上述等式的左边即为点的矩阵表示：点表示为前面 n 个元素为坐标系的系数，最后一个元素为 1 的行矩阵（也可以表示为列矩阵）
这种表示方式完全满足向量和点的运算，
// 点和向量的加法，向量 (1,1,1) 与点 (1,1,1)，结果最后一位为 1 表示点
(1, 1, 1, 1) + (1, 1, 1, 0) = (2, 2, 2, 1)
// 向量和向量的加法，结果最后一位为 0 表示向量
(1, 1, 1, 0) + (1, 1, 1, 0) = (2, 2, 2, 0)
...
是不是超级舒服？
可以用一组基向量，和一个原点描述一个坐标系。已经讲述了如何用矩阵表示向量和点了，我们可以直接代入，将前三行表示为基向量，第四行表示原点：
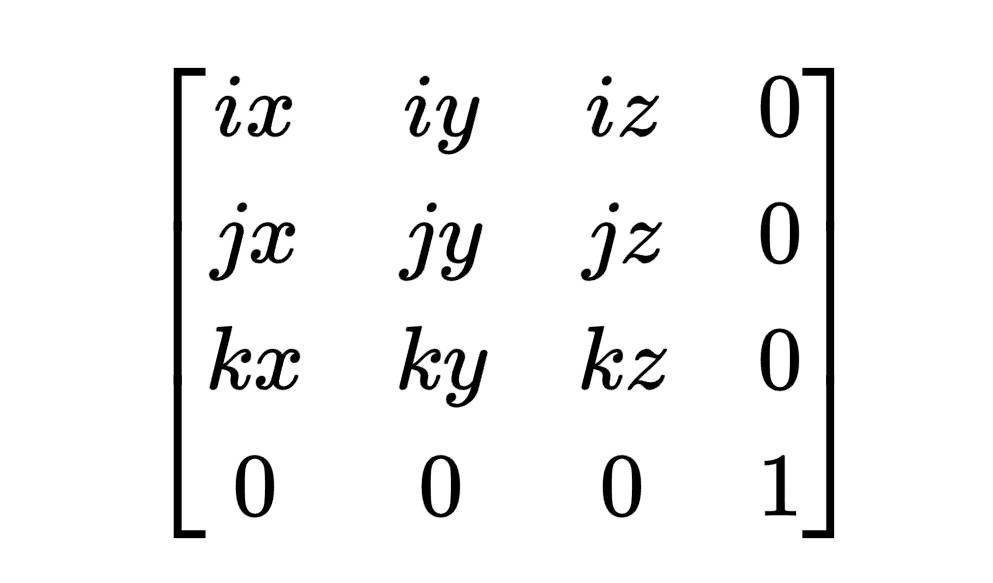
（完）