Home
GitHub
MiniCode
rss
日期：2021年7月12日标签：ComputerGraphics

颜色与冯氏光照模型 #

一. 颜色 #

中国色

中国色

在WebGL中，颜色用RGBA表示，每个值的取值范围从0到1，对应我们常用的取值范围0到255。例如在着色器中，想输出一个黑色：

void main() {
    FragColor = vec4(0.0, 0.0, 0.0, 1.0); // rgba(0, 0, 0, 1)
}

在真实世界中，我们肉眼看到的颜色，往往不是物体真正的颜色。真实世界中物体的反射的颜色一般会与环境有关，经过光线照射（太阳光，灯光），物体会反射与其本身颜色有一定差异的颜色，在白天和夜晚由于光线的强度不同，物体反射的颜色一般也不同。所以，了不起的前辈们用以下公式模拟计算出物体最终反射的颜色：

FragColor = ObjectColor * LightColor; // 将对应的rgba分量相乘，得到FragColor的rgba值

FragColor表示最终颜色，ObjectColor表示物体本身的颜色，LightColor表示光线的颜色。这个公式用于计算一个物体在某种颜色的灯光下反射的颜色，不同的灯光颜色会产生不同的结果颜色。例如如果物体是黑色的，那么它会吸收所有颜色的光，最终反射出黑色：

FragColor = vec4(0.0, 0.0, 0.0, 1.0) * LightColor; // 因为rgb为0，所以FragColor的rgb为0，显示为黑色。

再比如一个红色的物体（rgba(1, 0, 0, 1)），在太阳光下（太阳光我们认为其rgba为(1, 1, 1, 1)）,显示为红色：

FragColor = vec4(1.0, 0.0, 0.0, 1.0) * vec4(1.0, 1.0, 1.0, 1.0); // FragColor = vec4(1.0, 0.0, 0.0, 1.0)

FragColor = ObjectColor * LightColor在图形领域中，被称作颜色的反射定律。这种方式可能不能完全模拟真实世界的所有颜色，但是已经足够我们用来模拟一个非常真实的世界了。

二.冯氏光照模型 #

冯氏光照模型

图片来源于LearnOpenGL_CN

冯氏光照模型是处理现实世界复杂光照的一种模型，冯氏光照模型的主要结构由3个分量组成：环境(Ambient)、漫反射(Diffuse)和镜面(Specular)光照。

  • 环境光照（Ambient Lighting）：现实世界一般都不是完全黑暗的，即使在夜晚，也会有一点光亮（月光，远处的光），所以物体总会显示一点颜色，所以冯氏光照会使用一个比较小的环境光照常量，永远为物体提供一些颜色。
  • 漫反射光照（Diffuse Lighting）：模拟光线照射到物体表面的角度不同显示不同的颜色的现象，一般直射物体表面时，颜色越亮。
  • 镜面光照（Specular Lighting）：模拟表面光滑的物体在反射光线时，偶尔会出现镜面高光的现象。

利用冯氏光照模型，我们可以创建出非常有意思的场景了，接下来跟着我，来绘制一个光照下的立方体吧。

环境光照（Ambient Lighting） #

为了实现环境光照，只需要设置一个环境光因子，用环境光因子乘以光照，然后再将结果乘以物体颜色得到最终的片段着色器输出颜色。片段着色器glsl如下：

    #version 300 es
    precision highp float;

    out vec4 FragColor;

    uniform vec3 u_objColor; // 物体颜色
    uniform vec3 u_lightColor; // 光照颜色
    float ambientStrength = 0.1; // 环境光因子

    void main() {
        vec3 ambient = ambientStrength * u_lightColor;
        vec3 result = u_objColor * ambient;
        FragColor = vec4(result, 1.0);
    }

我后续的代码都是使用的WebGL2，与WebGL有一点差异，但是差异不是很大，不会WebGL2的朋友不必担心。作为冯氏光照的第一阶段，环境光照是是很弱的，所以这里环境因子我设置为0.1，只给物体提供一丢丢颜色。

接下来绘制一个立方体。立方体顶点数据可以在这里获得。接下来就是创建VAO（Vertext Array Data）、VBO（Vertex Array Buffer），给着色器传递数据了，这一过程比较简单我就不详细写下来了，可以参考源码：https://github.com/pengfeiw/webgl2-demos/blob/master/src/demos/theroyOfLight/phongLighting.ts。

const vertex_source =
    `#version 300 es

    in vec3  a_pos;

    uniform mat4 projection;
    uniform mat4 view;
    uniform mat4 model;

    void main() {
        gl_Position = projection * view * model * vec4(a_pos, 1.0);
    }
`;

const fragment_source =
    `#version 300 es
    precision highp float;

    out vec4 FragColor;

    uniform vec3 u_objColor; // 物体颜色
    uniform vec3 u_lightColor; // 光照颜色
    float ambientStrength = 0.1; // 环境光因子

    void main() {
        vec3 ambient = ambientStrength * u_lightColor;
        vec3 result = u_objColor * ambient;
        FragColor = vec4(result, 1.0);
    }
`;

const draw = (gl: WebGL2RenderingContext) => {
    const shader = new Shader(gl, vertex_source, fragment_source);

    // vao
    const vao = gl.createVertexArray();
    gl.bindVertexArray(vao);

    // vbo
    const vbo = gl.createBuffer();
    const posAttLocation = gl.getAttribLocation(shader.program, "a_pos");
    gl.bindBuffer(gl.ARRAY_BUFFER, vbo);
    gl.bufferData(gl.ARRAY_BUFFER, new Float32Array(verticesData), gl.STATIC_DRAW);
    gl.enableVertexAttribArray(posAttLocation);
    gl.vertexAttribPointer(posAttLocation, 3, gl.FLOAT, false, 0, 0);

    // uniform
    shader.useProgram();
    const model = mat4.create();
    shader.setMat4("model", model);

    shader.setFloat3("u_objColor", 0.36, 0.42, 0.60);
    shader.setFloat3("u_lightColor", 1.0, 1.0, 1.0);

    const camera = new Camera([0, 1, 4]);
    camera.mouseSensitivity = 0.04;
    var deltaTime = 0.01;
    var lastFrame = 0;
    const drawScene = (time: number) => {
        resizeCanvas(gl);

        const currentFrame = time;
        deltaTime = currentFrame - lastFrame;
        lastFrame = currentFrame;

        gl.enable(gl.DEPTH_TEST);
        gl.clearColor(0.0, 0.0, 0.0, 1.0);
        gl.clear(gl.COLOR_BUFFER_BIT | gl.DEPTH_BUFFER_BIT);

        gl.bindVertexArray(vao);
        shader.useProgram();
        const view = camera.getViewMatrix();
        shader.setMat4("view", view);

        const projection = mat4.perspective(mat4.create(), glMatrix.toRadian(camera.zoom), gl.canvas.width / gl.canvas.height, 0.1, 100);
        shader.setMat4("projection", projection);

        gl.drawArrays(gl.TRIANGLES, 0, 36);

        requestAnimationFrame(drawScene);
    };

    window.addEventListener("keydown", (event: KeyboardEvent) => {
        switch (event.key) {
            case "w":
                camera.processKeyboard(Camera_Movement.FORWARD, deltaTime * 0.001);
                break;
            case "s":
                camera.processKeyboard(Camera_Movement.BACKWARD, deltaTime * 0.001);
                break;
            case "a":
                camera.processKeyboard(Camera_Movement.LEFT, deltaTime * 0.001);
                break;
            case "d":
                camera.processKeyboard(Camera_Movement.RIGHT, deltaTime * 0.001);
                break;
            default:
                break;
        }
    });

    window.addEventListener("wheel", (event: WheelEvent) => {
        camera.processMouseScroll(event.deltaY * 0.01);
    });

    window.addEventListener("mousemove", (event: MouseEvent) => {
        camera.processMouseMovement(event.movementX, event.movementY);
    });

    requestAnimationFrame(drawScene);
};

代码里，我使用了我自己封装的Camera和Shader,这两部分我都详细讲述过，请参考：模拟一个摄像机、绘制一个三角形（shader程序创建）。

设置物体颜色与光照颜色：

shader.setFloat3("u_objColor", 0.36, 0.42, 0.60); // 淡蓝紫色
shader.setFloat3("u_lightColor", 1.0, 1.0, 1.0);  // 白色光

绘制结果如下，立方体仅仅有一点点颜色，表现很暗： 环境光照

冯氏光照第一阶段：环境光照对物体颜色的影响

漫反射光照（Diffuse Lighting） #

作为冯氏光照的第二阶段，漫反射光照对人的视觉产生的效果是最为显著的，也是最有意思的。请看下图：

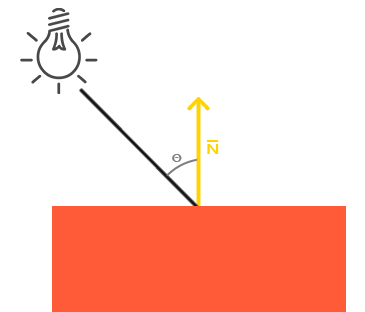
漫反射光照

图片来源于Learn_OpenGL_CN官网：漫反射光照示意图

光线逆方向与物体表面法向量有一个夹角，当夹角为0时，此时光照直射物体表面，光照强度最大，物体越亮，当夹角大于90度时，光照最小，物体表面颜色最暗。我们知道点积公式如下：

a·b = |a|*|b|*cos(angle)

由点积公式得到，当向量夹角为0时，点积最大，当夹角为90度时，点积为0。所以我们可以利用点积公式计算物体最终显示的颜色。要实现漫反射光照效果，首先我们需要知道每个顶点的法向量，由于立方体比较简单，我直接给出立方体的法向量数据，可以在这里获得顶点法向量的数据。在顶点着色器中增加法向量属性a_normal, 并利用v_normal传递给片段着色器

...
in vec3 a_normal;

out vec3 v_normal;

void main() {
    ...
    v_normal = a_normal;
}

在片段着色器中需要增加光照方向的全局变量：

uniform vec3 u_lightDirection; // 光照方向
in vec3 v_normal;

因为计算夹角，使用的是光照方向的相反方向，所以需要先计算光照的逆方向向量，并标准化向量：

vec3 lightDirectionReverse = normalize(vec3(-u_lightDirection.x, -u_lightDirection.y, -u_lightDirection.z));
vec3 normal = normalize(v_normal);

计算点积, 点积如果为负，取0值：

float diffuseStrength = max(dot(normal, lightDirectionReverse), 0.0);

计算漫反射分量，并更新输出颜色：

vec3 diffuse = diffuseStrength * u_lightColor;
vec3 result = u_objColor * (ambient + diffuse);
FragColor = vec4(result, 1.0);

完整的glsl如下：

// 顶点着色器
#version 300 es

in vec3  a_pos;
in vec3 a_normal;

out vec3 v_normal;

uniform mat4 projection;
uniform mat4 view;
uniform mat4 model;

void main() {
    gl_Position = projection * view * model * vec4(a_pos, 1.0);
    v_normal = a_normal;
}

// 片段着色器
#version 300 es
precision highp float;

in vec3 v_normal;

out vec4 FragColor;

uniform vec3 u_objColor; // 物体颜色
uniform vec3 u_lightColor; // 光照颜色
uniform vec3 u_lightDirection; // 光照方向
float ambientStrength = 0.1; // 环境光因子

void main() {
    // 环境光照
    vec3 ambient = ambientStrength * u_lightColor;
    
    // 漫反射
    vec3 lightDirectionReverse = normalize(vec3(-u_lightDirection.x, -u_lightDirection.y, -u_lightDirection.z));
    vec3 normal = normalize(v_normal);
    float diffuseStrength = max(dot(normal, lightDirectionReverse), 0.0);
    vec3 diffuse = diffuseStrength * u_lightColor;

    vec3 result = u_objColor * (ambient + diffuse);
    FragColor = vec4(result, 1.0);
}

在绘制代码，我们需要增加传递法向量数据，创建缓冲传递数：

const normalVbo = gl.createBuffer();
const normalAttLocation = gl.getAttribLocation(shader.program, "a_normal");
gl.bindBuffer(gl.ARRAY_BUFFER, normalVbo);
gl.bufferData(gl.ARRAY_BUFFER, new Float32Array(normals), gl.STATIC_DRAW);
gl.enableVertexAttribArray(normalAttLocation);
gl.vertexAttribPointer(normalAttLocation, 3, gl.FLOAT, false, 0, 0);

设置光照方向：

shader.setFloat3("u_lightDirection", 1.0, -0.5, -1.0);

然后，你应该能绘制出如下的情景，不同的面颜色亮度不一样： 漫反射

镜面光照（Specular Lighting） #

冯氏光照的最后一个阶段，只有把镜面高光加入到我们的绘制场景中，才算一个完整的冯氏光照。

在现实世界中，在一个阳光明媚的下午，你看向一个表面光滑的物体，比如镜子，站在某个位置，你会被物体表面反射的强光闪到眼睛，因为某一块特别的亮，这种现象叫做镜面光照，这就是冯氏光照第三阶段需要处理的情况，与漫反射一样，这一阶段也是利用了点积的思想。

镜面光照

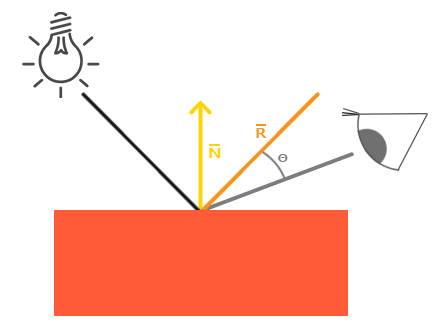
图片来源于LearnOpenGL_CN

从图中可以看到，光线照射到物体表面，会反射出一个光线，我们称这个为反射光，反射光与我们视线形成一个夹角，当这个夹角为0时，我们就会产生刺眼的效果，所以夹角越小，镜面光照的影响越大。

为了计算镜面光照，我们需要以下两个方向向量：

  • 视线方向
  • 反射光的方向

视线的方向可以通过片段位置和摄像机的位置计算得出，反射光的方向可以通过法向量和光照方向计算得出。在片段着色器中增加摄像机位置全局变量：

uniform vec3 viewPos; // 摄像机位置

shader.setFloat3("viewPos", camera.position[0], camera.position[1], camera.position[2]);

将片段位置从顶点着色器中传递到片段着色器中：

// 顶点着色器
out vec3 v_pos;
void main() {
    v_pos = (model * vec4(a_pos, 1.0)).xyz;
}

// 片段着色器
in vec3 v_pos;

计算镜面光照,利用glsl中的reflect函数可以直接计算反射向量：

// 镜面光照
vec3 viewDir = normalize(viewPos - v_pos); // 观察方向向量
vec3 reflectDir = reflect(u_lightDirection, normal); // 光的反射向量，利用reflect函数计算
float spec = pow(max(dot(viewDir, reflectDir), 0.0), 30.0); // 30.0是高光的反光度
vec3 specular = specularStrength * spec * u_lightColor;

上面有一个物体反光度的概念，这里设置为30.0，一个物体的反光度越高，反射光的能力越强，散射得越少，高光点就会越小。我后面介绍物体材质时，会详细讲解反光度。

更新FragColor:

vec3 result = u_objColor * (ambient + diffuse + specular);
FragColor = vec4(result, 1.0);

如果你的代码, 没有错误，应该能看到如下的反光效果：

镜面光照

完整代码请参阅：theroyOfLight/phongLighting.ts。

（完）

上一篇：【WebGL】模拟摄像机下一篇：webgl模拟太阳系动画
目录
颜色与冯氏光照模型
一. 颜色
二.冯氏光照模型
环境光照（Ambient Lighting）
漫反射光照（Diffuse Lighting）
镜面光照（Specular Lighting）