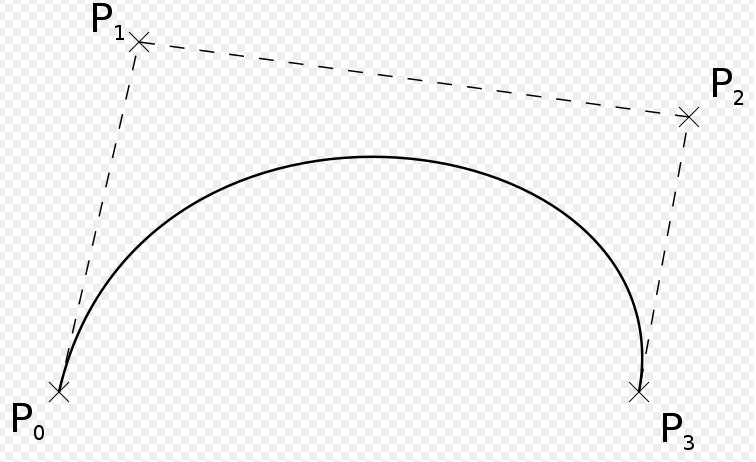
贝塞尔曲线在计算机图形学中应用十分广泛，photoshop、inkscape等主流设计软件中的钢笔工具都是通过贝塞尔曲线实现的，软件为了实现汉字的笔锋也需要借助贝塞尔曲线，前端Canvas API、SVG、threejs等图形相关的库都有贝塞尔曲线的身影，所以在图形学的道路上不可避免会与贝塞尔曲线打交道。
本文，尽量用简单的方式阐述贝塞尔曲线的秘密。
三次贝塞尔曲线在线演示：https://www.geogebra.org/m/xejwa6xx
贝塞尔曲线的定义由贝塞尔的控制点个数决定，可能有2个、3个、4个，甚至更多定义点。有两个控制点的贝塞尔曲线，称之为一次贝塞尔曲线，同理3个控制点和4个控制点，被称为二次贝塞尔曲线和三次贝塞尔曲线...
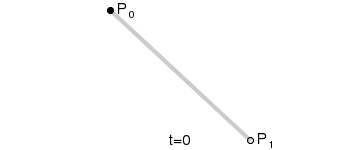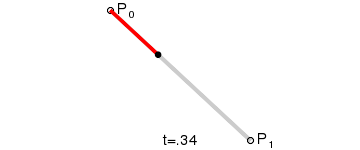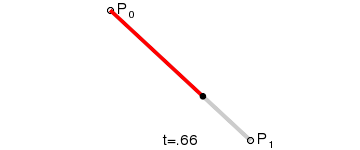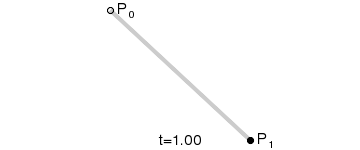
一次贝塞尔曲线有两个控制点，因为是一次曲线，所以它是个直线（段）。
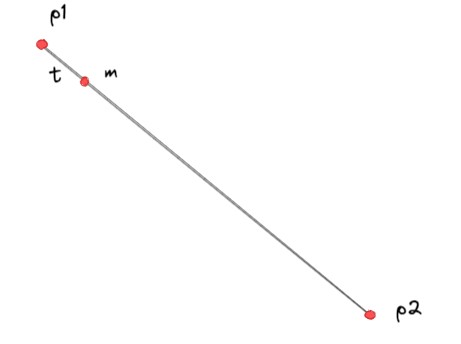
如图，p1和p2是控制点，m为构成贝塞尔曲线的点，满足0 <= t <= 1，当t等于0时，m点与p1点重合，当t等于1时，m点与p2点重合。所有符合条件的m点构成了控制点p1和p2决定的贝塞尔曲线，最终结果就是p1p2直线段。
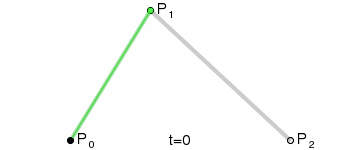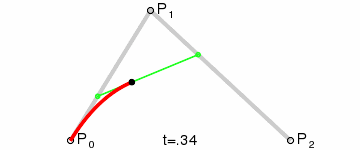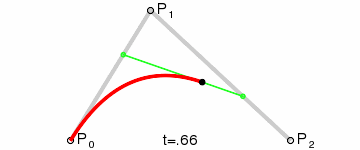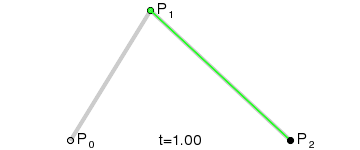
二次贝塞尔曲线有三个控制点p0、p1、p2，它是一个曲线。
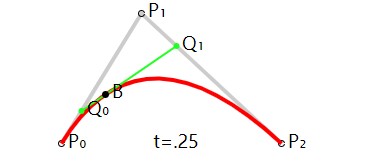
二次贝塞尔曲线满足的条件是：
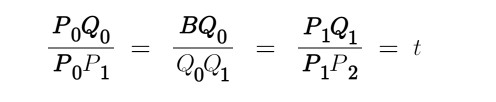
其中t满足0 <= t <= 1，当t从0-1之间变化时，得到的所有的B点构成的曲线称之为由控制点p0、p1、p2决定的二次贝塞尔曲线。
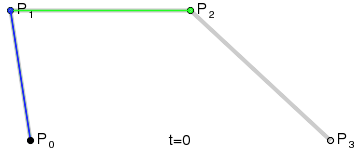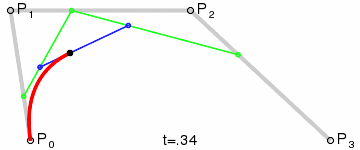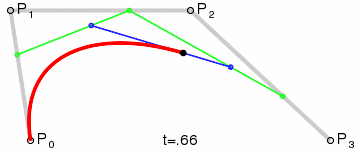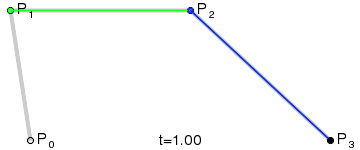
三次贝塞尔曲线有四个控制点p0、p1、p2和p3。
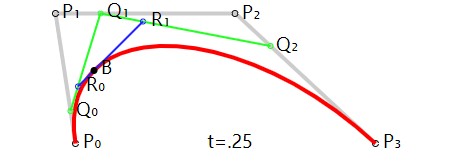
与二次贝塞尔曲线类似，三次贝塞尔曲线满足的条件是：
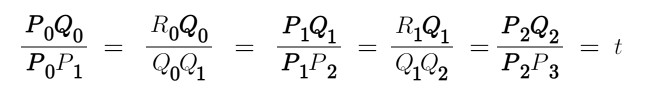
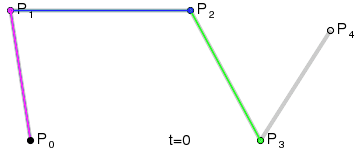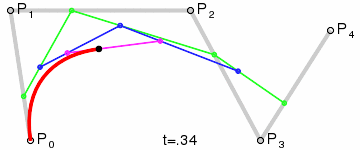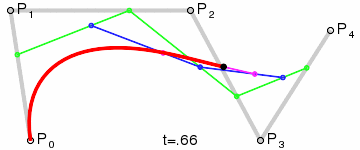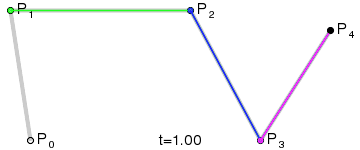
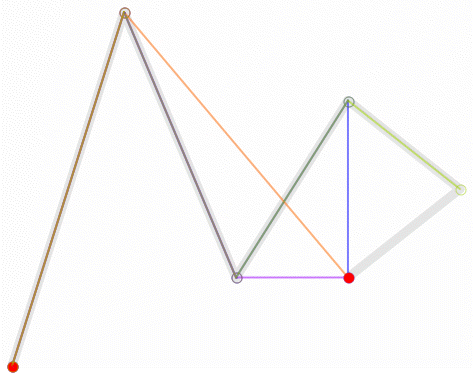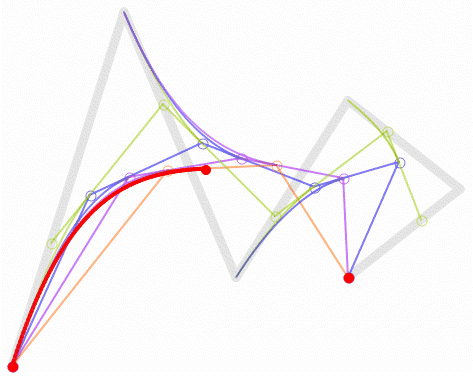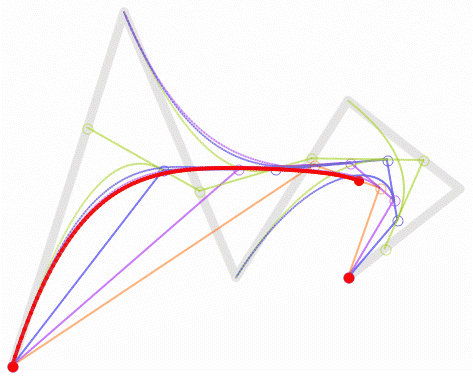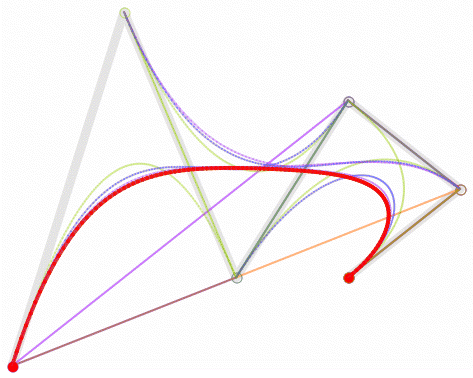
其中t满足0 <= t <= 1，当t从0-1之间变化时，得到的所有的B点构成的曲线称之为由控制点p0、p1、p2和p3决定的三次贝塞尔曲线。
高阶贝塞尔曲线的形成方式和低阶贝塞尔曲线一样，只是控制点的个数不一样，例如四次、五次。
贝塞尔曲线，在图形学中应用十分广泛，如果想要用代码绘制出漂亮的弧线，贝塞尔曲线应该能够产生作用。其中二次和三次目前是应用最为广泛的，很多软件的钢笔工具就是使用的二次贝塞尔曲线和三次贝塞尔曲线，Canvas API和svg中都使用到了三次贝塞尔，osg、threejs等图形库，也用到了三次贝塞尔曲线来绘制弧线和曲面。
最后给大家推荐一个不错的网站cubic-bezier。
（完）
