拉格朗日插值法 #

在前一篇文章介绍了艾特肯算法，本节继续介绍另一种曲线插值算法，拉格朗日插值法（Lagrange interpolatoion）。

算法思想 #

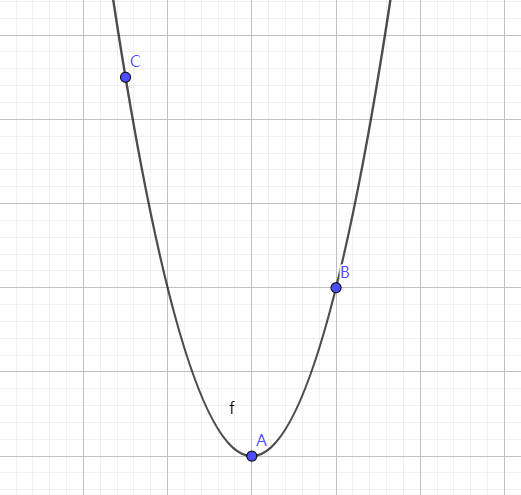
求过三点的曲线

可以在这里互动体验拉格朗日插值法：拉格朗日插值法。

本节内容以平面曲线为例，假设有三个点 $(x_1, y_1), (x_2, y_2), (x_3, y_3)$ ，我们希望能够获得一条曲线能够通过这三个点，假设这条曲线的多项式为：

y = a + bx + cx^2

将三个点带入上面的二次多项式得到：

y_1 = a + bx_1 + cx_1^2 \\ y_2 = a + bx_2 + cx_2^2 \\ y_3 = a + bx_3 + cx_3^2 \\

显然我们可以通过上面的三个方程组，求得 $a, b, c$ 的值，但是这种方法这并不是本篇文章的重点，重点是如何用拉格朗日法求曲线。

那么拉格朗日是如何思考这个问题的？首先要明确的是要计算的曲线一定是一个二次曲线，拉格朗日希望通过三根二次曲线的合并得到目标曲线。

第一根曲线在 $x_1$ 点处取值为 1，在 $x_2$ 和 $x_3$ 时取值为 0。

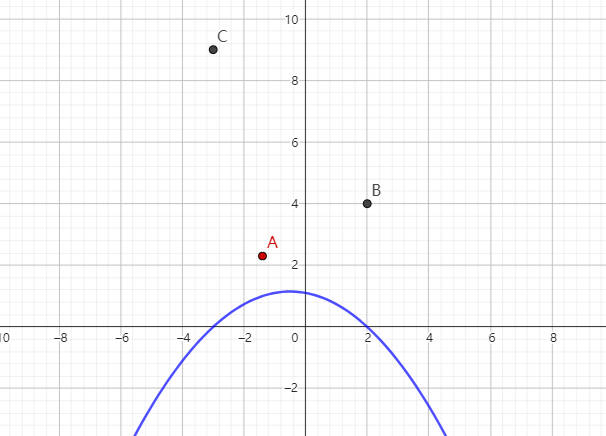
拉格朗日的第一根曲线

第二根曲线在 $x_2$ 点取值为 1，在 $x_1$ 和 $x_3$ 处取值为 0。

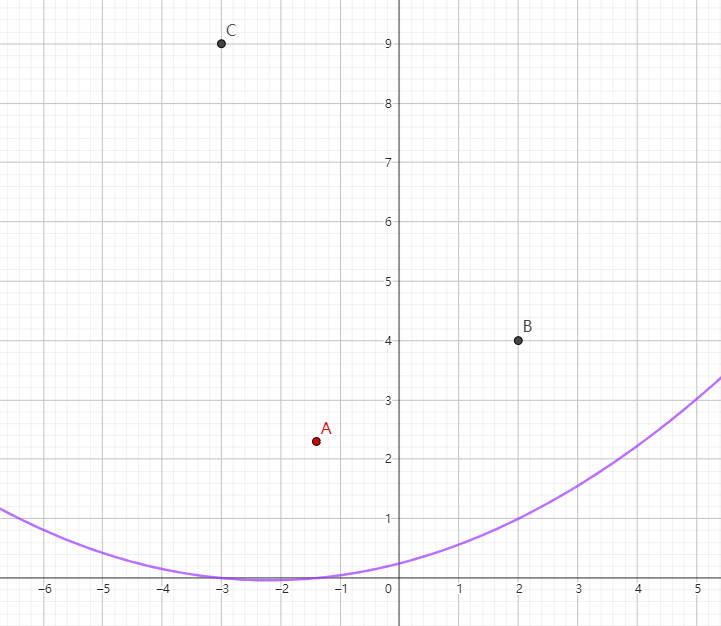
拉个朗日的第二根曲线

第三根曲线在 $x_3$ 点取值为 1，在 $x_1$ 和 $x_2$ 处取值为 0。

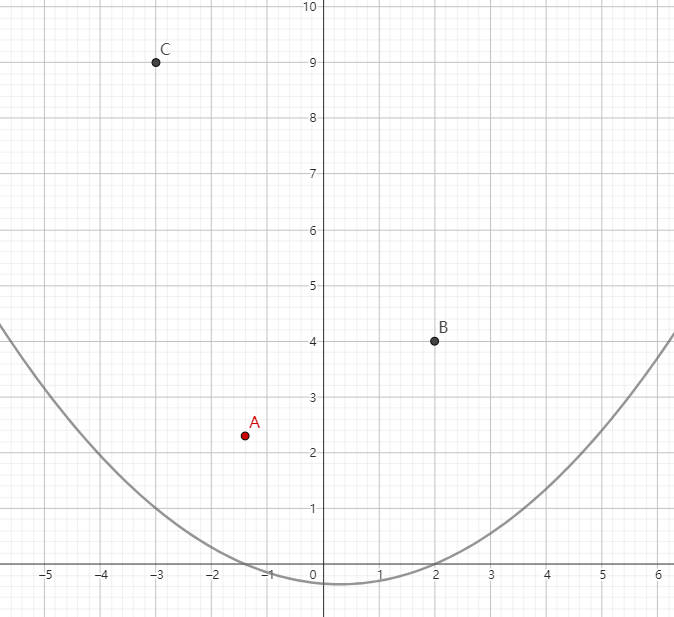
拉个朗日的第三根曲线

假设这三根曲线方程记为 $f_i(x)$ ，则有以下推论成立。

将上述三个曲线 $y_if_i(x)$ 合并即可求得最终经过三个点的曲线。

f(x) = y_1f_1(x)+ y_2f_2(x) + y_3f_3(x)

这就是拉格朗日的核心思想。

那么 $f_i(x)$ 应该是一个什么样的方程？ $f_i(x)$ 必须满足如下条件：

f_i(x_j) = \begin{cases} 1 \quad i = j \\ 0 \quad i \neq j \end{cases}

构造 f_1(x) 的方程如下，很显然可以满足上述条件：

f_1(x) = \frac{(x - x_2)(x - x_3)}{(x_1 - x_2)(x_1 - x_3)}

推导到一般情况， $f_i(x)$ 的方程如下：

f_i(x) = \prod_{j \neq i}^{1 \leq j \leq 3}\frac{x - x_j}{x_i - x_j}

最终能够得到拉格朗日插值公式：

f(x) = \sum_{i = 1}{3}y_i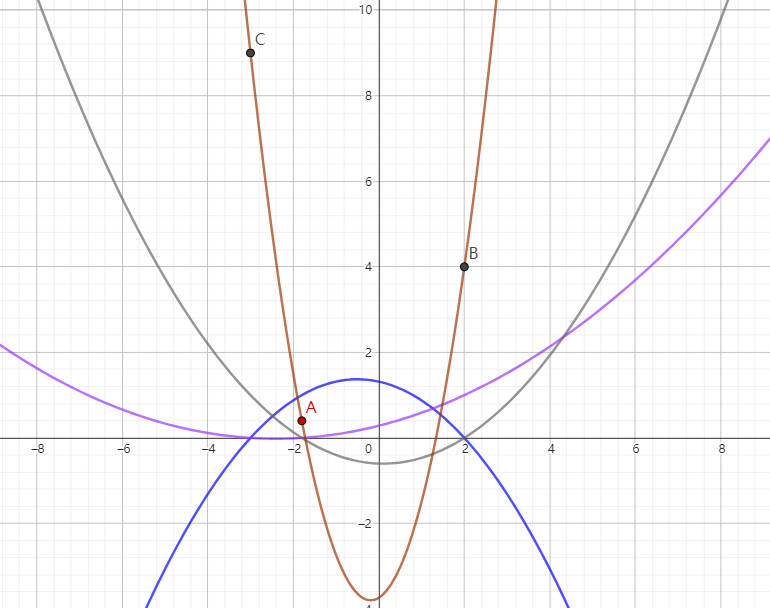f_i(x)

拉格朗日插值法合并后的曲线

拉格朗日插值法和艾特肯算法一样，也出现了“失控”的点，不能很好的控制曲线的形状。

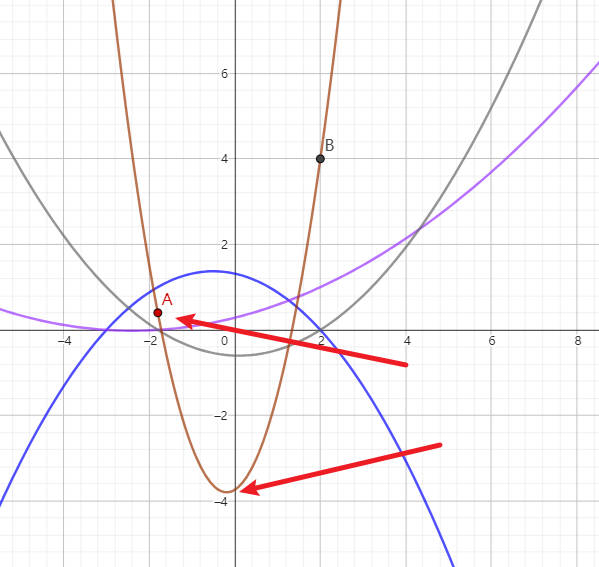
拉格朗日法的缺点

所以建模一般很少采用这种曲线算法。

（完）