曲线插值之艾特肯算法 #

曲线插值是计算机图形学中使用的一种曲线近似方法，你可能在设计工具中使用过设计曲线功能，例如绘制贝塞尔曲线或者 b 样条曲线，通过调整几个控制点来绘制曲线，这些都用到曲线插值算法。所以这里介绍艾特肯插值算法（Aitken's Algorithm）。

多项式曲线插值 #

何为多项式曲线插值？你肯定知道线性插值（Linear Interpolation），就是给定两个点 $(x_0, y_0)$ 和 $(x_1, y_1)$ 在这两点之间的连线上确定一个未知点。

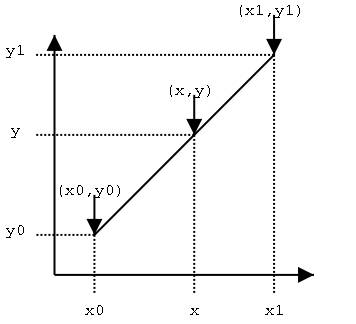
利用等比关系：

很容易得到，线性插值的公式为：

艾特肯算法 #

艾特肯算法是一种曲线近似方法，通过给定控制点，计算控制点间的插值点来模拟曲线。

在计算机图形学中，曲线一般用参数化方程表示。3D 中最常用的是三次曲线方程，形式如下：

这里就不过多介绍参数化曲线方程的概念了，这并不是本节内容的目的，如果有需要可以看看这篇文章：https://pages.mtu.edu/~shene/COURSES/cs3621/NOTES/curves/curves.html

艾特肯的算法思想是递归，将复杂的问题，分为两个简单的问题，分别解决这两个简单的问题，然后合并简单问题的解决方案得到复杂问题的解决方案。

假设有 n 个控制点，艾特肯算法将复杂的插值问题拆分如下：

• 抛弃最后一个控制点，计算前 n - 1 个控制点的插值曲线
• 抛弃第一个控制点，计算后 n - 1 个控制点的插值曲线

最后合并（blender） 上述两段曲线。如果前 n - 1 个控制点的插值曲线的计算仍然复杂，可以继续按照上述思路递归分解合并，分解直到只有两个控制点时，使用线性插值的方式，计算插值曲线。

为了简化问题，这里我们只看 $y$ 分量即可，因为针对的是参数方程，$x$ 坐标的插值算法是与 $y$ 相同的。 因为分解问题后，我们在控制点间能得到很多段线段，我们用 $y_i^1(t)$ 表示 $y_i$ 和 $y_{i+1}$ 之间的线段，使用 $y_i^2(t)$ 表示 $y_i$ 和 $y_{i+2}$ 之间的二次曲线。

先看一个简单的例子，假设有三个控制点 $(t_1, y_1), (t_2,y_2),(t_3, y_3)$。$y_1^2(t)$ 是 $y_1, y_2, y_3$ 的插值曲线，它是由 $y_1^1(t)$ 和 $y_2^1(t)$ 合并得到。

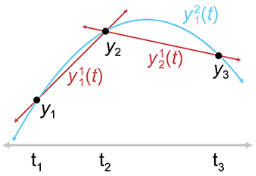
由线性插值算法能够得到第一段和第二段线段的方程：

二次曲线 $y_1^2(t)$ 的公式，仅仅是在 $y_1^1(t)$ 和 $y_2^1(t)$ 进行线性插值即可。

艾特肯算法的通用公式如下：

不足之处 #

在本篇最后我们希望通过艾特肯算法模拟下图中的曲线，这是一个横着的 S 曲线。

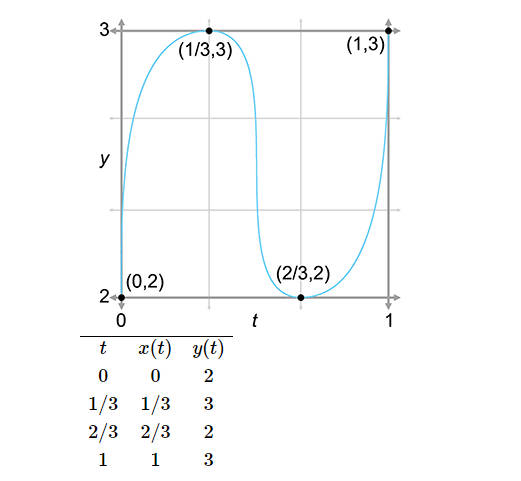
通过艾特肯算法模拟后，结果如下。

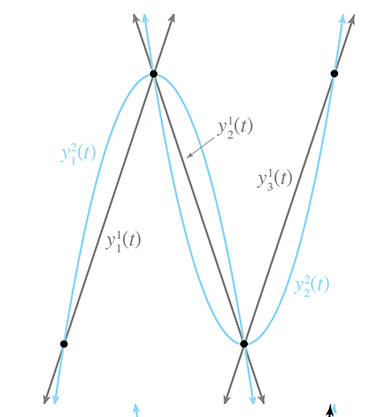
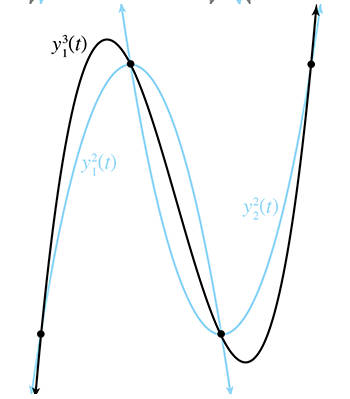
可以看到通过艾特肯算法，控制点好像并不能真的能控制曲线的形状，第二个第三个控制点貌似失控了，这往往并不是我们想要的结果，所以设计工具中艾特肯插值曲线并不流行。

（完）