计算机内部使用数字电路搭建而成,而数字电路由 0 和 1 两种状态组成,所以计算机内部的沟通都是通过 0 和 1 沟通。十进制是“逢十进一“,二进制则是“逢二进一“。
例如,二进制 11 表示 十进制的 3,三位二进制最大能表示的数字为 111,即十进制的 7。关于十进制与二进制的转换不在本节内容的讨论范围内,请读者另外查找资料。
下面是一位二进制的加法表:
| op1 | op2 | res |
|---|---|---|
| 0 | 0 | 00 |
| 1 | 0 | 01 |
| 0 | 1 | 01 |
| 1 | 1 | 10 |
计算机采用的是如下逻辑电路计算两个 bit 的加法。
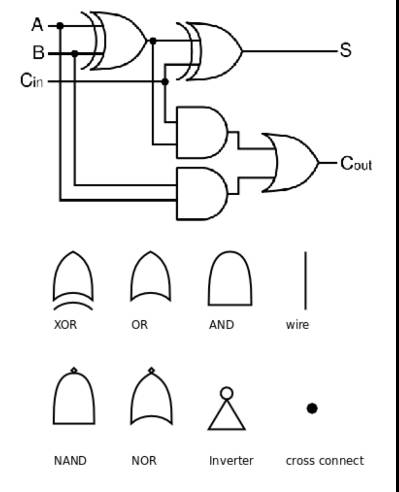 全加器以及相关符号表示
全加器以及相关符号表示
要理解全加器,首先要理解里面的符号表示:XOR(异或),OR(或),AND(与),NAND(非与),NOR(非或),Inverter(取反)。
各种符号运算方法如下:
通过上述方法,我们可以列出每种运算方法的真值表,例如 XOR 的真值表如下:
| A | B | A XOR B |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 0 |
感兴趣的朋友可以自己列出其他几种运算的真值表。
接下来,再对照上图中的全加器数字电路图,看看它是如何实现的,图中 Cin 是低位传上来的进位,Cout 是产生的进位,例如 1 和 1 进行 AND 运算(这里的 1 表示第 0 位),产生的 Cout 为 1,但是对于第 1 位来说低位产生的 Cout 则是高位的 Cin。
我们列出全加器的真值表:
| A | B | Cin | Cout | S |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 |
请读者自己根据上面的表和全加器图进行对照运算,以理解全加器的工作原理。
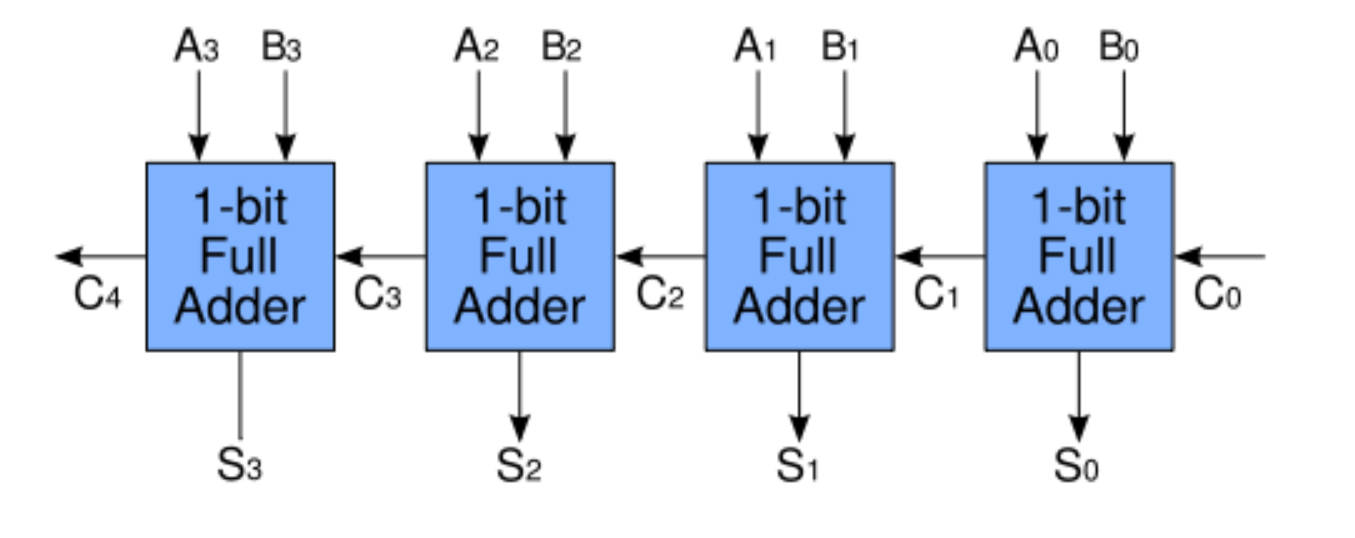
有了全加器,我们将很多个一位全加器串联,就得到了多位加法器。
(完)