日期:2021年4月2日标签:Algorithm/Math
递归 #
一. 递归的含义 #
递归(英语:Recursion),又译为递回,在数学与计算机科学中,是指在函数的定义中使用函数自身的方法。
维基百科有几个语言例子,我觉得挺有意思:
- 从前有座山,山里有座庙,庙里有个老和尚,正在给小和尚讲故事呢!故事是什么呢?“从前有座山,山里有座庙,庙里有个老和尚,正在给小和尚讲故事呢!故事是什么呢?‘从前有座山,山里有座庙,庙里有个老和尚,正在给小和尚讲故事呢!故事是什么呢?……’”
- 一只狗来到厨房,偷走一小块面包。厨子举起杓子,把那只狗打死了。于是所有的狗都跑来了,给那只狗掘了一个坟墓,还在墓碑上刻了墓志铭,让未来的狗可以看到:“一只狗来到厨房,偷走一小块面包。厨子举起杓子,把那只狗打死了。于是所有的狗都跑来了,给那只狗掘了一个坟墓,还在墓碑上刻了墓志铭,让未来的狗可以看到:‘一只狗来到厨房,偷走一小块面包。厨子举起杓子,把那只狗打死了。于是所有的狗都跑来了,给那只狗掘了一个坟墓,还在墓碑上刻了墓志铭,让未来的狗可以看到……’”
- 大雄在房里,用时光电视看着从前的情况。电视画面中的那个时候,他正在房里,用时光电视,看着从前的情况。电视画面中的电视画面的那个时候,他正在房里,用时光电视,看着从前的情况……
可以看出递归实际就是循环,不过是程序一遍又一遍的调用自身,然后递归程序必须有一个退出循环的条件,否则就会导致死循环。
二.走楼梯 #
有一个经典的算法题,问一个10级台阶的楼梯,如果每次只能走一个台阶或者两个台阶,那么有多少种走法? 很多人看过很多次这种题目,所以很快的写出如下答案:
function solution(n) {
if (n === 1) return 1;
if (n === 2) return 2;
return solution(n - 1) + solution(n - 2);
}
solution(10);
该解法,就用了递归的思想,因为一个人每走一次,有两种走法,可以走两个台阶,也可以走一个台阶。所以在n台阶上,他前一步可能在n-1台阶上,也可能在n-2台阶上。假设要到达n-1台阶上,有solution(n-1)种走法,到达n-2台阶有solution(n-2)种走法,那么到达n台阶,有solution(n-1) + solution(n-2)种走法。
注意我上面的解答给出了递归终止点:
if (n === 1) return 1;
if (n === 2) return 2;
如果没有这两句,程序将会进入死循环,导致内存溢出。
相信大家在看到题目时,都会很容易的写出上面的答案,但是上面的解法效率并不高。
三.正向解法 #
上面的走楼梯有没有更好的解法呢?能不能优化算法的效率呢?请仔细想一想。
如果我们分析solution(n-1)+solution(n-2)的递归树,会发现里面有大量的重复计算,时间复杂度是以n的指数增长的。我们以solution(5)为例:
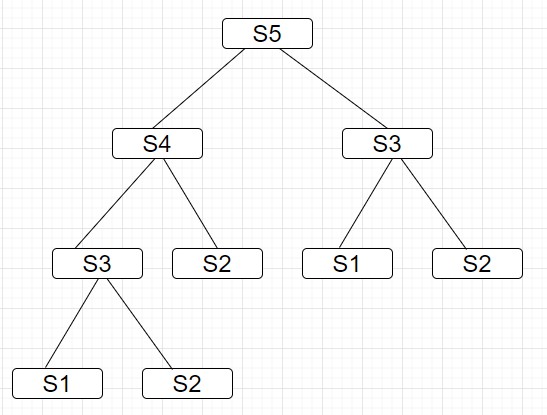
可以看到solution(3)需要重复两次计算,solution(2)需要重复3次,solution(1)重复两次。
我们将上面的解法,反过来求解,先求s1,在求s2,在通过s1和s2求s3,然后依次求s4、s5...这样算法的复杂度为n。然后我们可以写出如下代码:
function solution(n) {
if (n === 1) {
return 1;
}
if (n === 2) {
return 2;
}
var a = 1, b = 2, index = 3;
while(index < n) {
var tem = a;
a = b;
b = tem + b;
index++;
}
return a + b;
}
(完)