点到直线的距离 #

本文介绍直线的表示方式，以及如何计算一个点到直线的距离。

直线的表示方式 #

参数化形式 #

直线的参数化形式是通过直线的方向向量定义的，假设直线的方向向量为 $\vec{d}$，直线上有一点 $P$，则直线上的任意一点都存在一个 $t$，可以使点用 $P + t \vec{d}$表示。

所以直线的参数化形式为：

对于射线，也可以用这个公式表示，只不过射线的参数满足 $t > 0$。

隐含形式 #

假设直线的法向量是 $\vec{n}$，直线上的某个点用 $X = (x_0, x_1)$ 表示，如果点 $P$ 是直线上的一个点，则向量 $\overrightarrow{PX}$与 $\vec{n}$的点积为 0。即 $\vec{n} \cdot (X - P) = \vec{n} \cdot X - \vec{n} \cdot P = 0$，另 $\vec{n} \cdot P = d$，则可得到：

这就是直线的隐含表示方式（法线形式）。

点到直线的距离 #

参数化形式 #

对于参数化直线方程 $X(t) = P + t \vec{d}$，要计算点到直线的距离，就是要计算点到其再直线上的投影点的距离，例如下图中点 $Y$ 到 $X(\overline{t})$ 的距离。

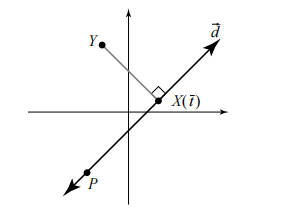
首先要明确的是 $Y - X(\overline{t})$ 一定是垂直与直线向量 $\vec{d}$的，所以两个向量的点积为 $0$。

所以投影点的参数 $\overline{t} = \vec{d} \cdot (Y - P) / {|\vec{d}|}^2$。

所以点到直线的距离的平方就是 ${|Y - (P + \overline{t}\vec{d})|} ^ 2$。

隐含形式 #

如果直线的方程是用法向量表示的 $\vec{n} \cdot X = c$，点到直线上最近的一个点 $K$，一定存在一个 $s$ 满足 $Y = K + s\vec{n}$，将等式两边点乘一个 $\vec{n}$得到 $\vec{n} \cdot Y = \vec{n} \cdot K + s {|\vec{n}|}^2 = c + s{|\vec{n}|}^2$，所以 $s = (\vec{n} \cdot Y - c)/{|n|}^2$。

点到直线的距离为 $|Y - K| = |s||\vec{n}|$，即：

如果法向量是单位向量，上述公式简化为：

点到射线的距离 #

当能够计算点到直线的距离时，点到射线的距离也就很容易计算了。射线上的起点为 $P$，方向向量为 $\vec{d}$。

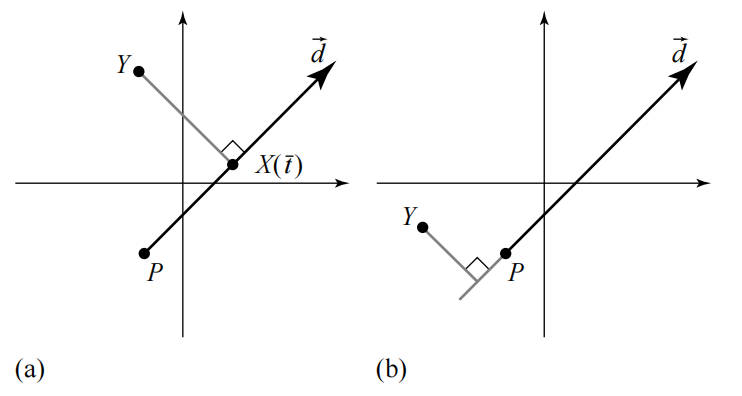
• $\vec{d} \cdot (Y - P) > 0$: 如果点 $Y$ 的投影点 $X(\overline{t})$ 在射线上时，点到射线的最近点就是投影点 $X(\vec{t})$，如上图 a 所示。
• $\vec{d} \cdot (Y - P) \leq 0$：如果点 $Y$ 的投影点 $X(\overline{t})$ 不在射线上时，点到射线的最近点就是射线的起点 $P$，如上图 b 所示。

点到线段的距离 #

点到线段的距离分为三种情况。点的投影点 $\overline(t)$ 可能在线段的起点前、终点后或者落到线段上。

• 投影点 $\overline(t)$ 在起点前，点到线段的最近点为起点
• 投影点 $\overline(t)$ 在终点后，点到线段的最近点为终点
• 投影点 $\overline(t)$ 在线段上，到店线段的最近点为 $\overline(t)$

点到凸多边形的距离 #

计算点 $X$ 到多边形的距离就变得十分简单，只需要计算点 $X$ 到每条边的距离，然后取最小值即可。

这样简单粗暴的方式并不是这里要说明的。凸多边形（convex polygon）有一个性质，对于凸多边形外的点，凸多边形总有一些边对点是不可见的，所以计算点到凸多边形的距离，只需要计算点到可见边的最小距离。

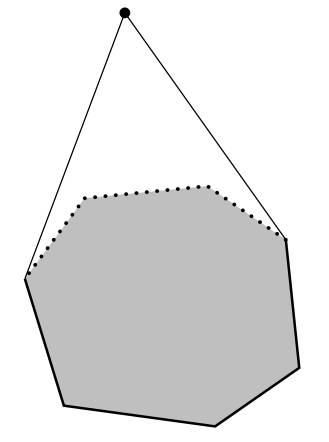
图中可见边用虚线表示，不可见边用实线表示。所以问题就变成了过滤不可见边。

假设凸多边形由 $P_0 \cdot P_n$ 表示，每条边 $P_iP_{i+1}$ 都有一个指向凸多边形内部的法向量 $n_i$，如果一条边满足 $(X - P_i) \cdot n_i < 0$ 则该边就是可见边。

这种利用点积过滤的方式，速度非常快，避免了计算每条边到点 $X$ 的距离。

另一种判断可见边的方式是，画一条线段 $XP_i$，如果 $XP_i$ 与凸多边形的某条边相交则表示该边是不可见边，但是该算法需要计算线段线段相交性，速度不快，所以不提倡用这种方式。

（完）