常见的函数图像 #

一. 函数的性质 #
首先讲述下函数的几种性质,设函数为 f(x),定义域为 D。
- 有界性
若存在 k1,在定义域内的所有 x 满足, f(x) <= k1,则 k1 为函数的上界。
若存在 k2,在定义域内的所有 x 满足, f(x) >= k2,则 k2 为函数的下界。
- 单调性
如果函数上任意两点 x1 和 x2,当 x1 < x2 时,恒有 f(x1) < f(x2),称函数是单调增加的,若恒有 f(x1) > f(x2),称函数是单调减小的。
- 奇偶性
当函数的定义域关于原点对称,并且 f(-x) = f(x),那么 f(x) 为偶函数。
当函数的定义域关于原点对称,并且 f(-x) = -f(x),那么 f(x) 为奇函数。
当函数的定义域不关于原点堆成,那么 f(x) 非奇非偶。
- 周期性
如果存在一个正数 l,使得对任意定义域内的 x 和 x + l,满足 f(x + l) = f(x),那么称 f(x) 为周期函数。通常我们说周期函数的周期是指最小正周期。
二. 函数的导数 #
分析函数图像,我是通过函数的导数分析的。三次函数求导后变成了二次,二次变成了一次,关于如何求导,可以自行百度。这里,我只说明导数是如何影响函数图像的。
当某一点的导数大于0,此时该点处的切线方向是递增方向的,即由第三象限指向第一象限。当导数等于0,切线方向为水平方向。当导数小于0,切线方向是递减方向。因此可以从某一点的导数判断此时函数图像是递增还是递减的。
接下来,我们借助函数的导数从函数的有界性、单调性、奇偶性和周期性分析一些常见的函数。
三. 一次函数 #
一次函数指的是形为 f(x) = ax + b (a 不等于 0)的函数,例如 f(x) = x + 1,它的函数图像如下。
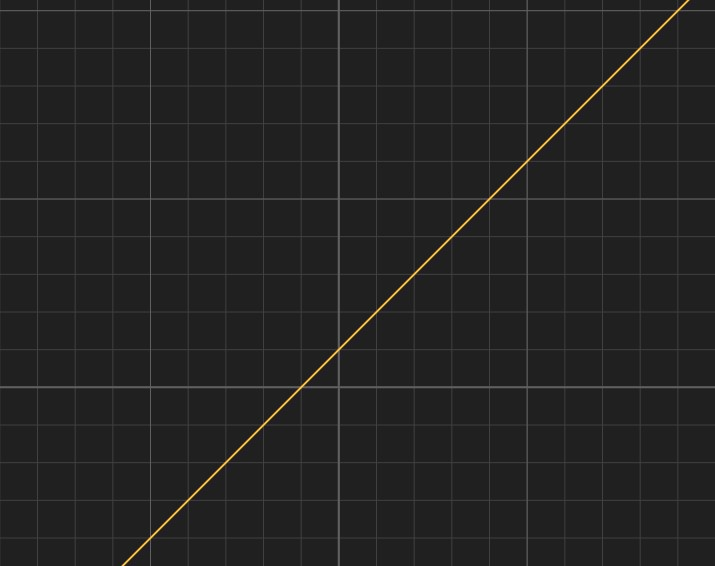
- 有界性
因为 a != 0,所以函数无界。
- 单调性
当 a > 0 时,函数单调递增的,当 a < 0 时,函数单调递减。
- 奇偶性
当 b = 0 时,此时函数图像经过原点,此时为奇函数。
当 b != 0 时,此时函数非奇非偶。
- 周期性
一次函数无周期性。
四. 二次函数 #
二次函数是描述抛物线的数学表达式,指的是形为 f(x) = ax² + bx + c(a 不等于 0)的函数,例如 f(x) = x² + 3。
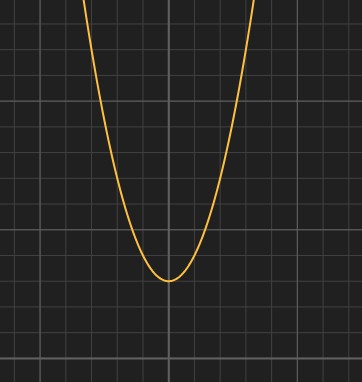
- 有界性
二次函数有界,当 a > 0 时,有下界,反之有上界。
当 a > 0 时,二次函数开口向上,所以最小值为谷底,当 x = -b / (2a) 时,函数取得最小值 c。
当 a < 0 时,二次函数开口向下,所以最小值为峰顶,当 x = -b / (2a) 时,函数取得最大值 c。
计算函数最大值和最小值可以通过函数求导得到。
- 单调性
当 a > 0 时,二次函数开口向上,当 x < -b / (2a) 时,函数递减,当 x > -b / (2a),函数递增。
当 a < 0 时,二次函数开口向下,当 x < -b / (2a) 时,函数递增,当 x > -b / (2a),函数递减。
- 奇偶性
二次函数总是关于 x = -b / (2a) 对称,所以当 b != 0 时,函数非奇非偶。
当 b = 0 时 满足 f(x) = f(-x),所以函数为偶函数。
- 周期性
二次函数无周期性。
五. 三次函数 #
指的是形为 f(x) = ax³ + bx² + cx + d(a 不等于 0)的函数,例如 f(x) = x³,它的图像如下。
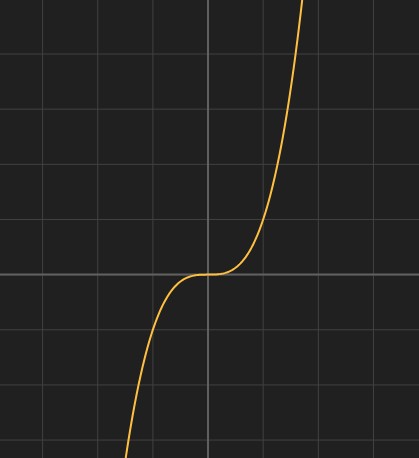
三次函数的导数为二次函数 f(x)',因为二次函数当 y 等于 0 时,可能的解的情况有 0、1 或者 2 个,所以三次函数的图像比较复杂。可能的情况有:
f(x)' <= 0 恒成立 #
- 有界性
无界。
- 单调性
函数递减。
- 奇偶性
可能为奇函数,也可能非奇非偶,例如 f(x) = -x³ 为奇函数,f(x) = -x³ + 3 非奇非偶。
- 周期性
无。
f(x)' >= 0 恒成立 #
- 有界性
无界。
- 单调性
函数递增。
- 奇偶性
可能为奇函数,也可能非奇非偶,例如 f(x) = x³ 为奇函数,f(x) = x³ + 3 非奇非偶。
- 周期性
无。
f(x)' = 0 有两个解 #
此时根据 f(x)' 函数的开口方向,f(x) 的递增递减顺序不同。当 f(x)' 函数开口向上时,导数先大于0,然后小于0,最后大于0,所以 f(x) 函数图像的变化是递增 -> 递减 -> 递增,你因该能想象它的形状类似于字母 N 。反之当 f(x)' 函数开口向下时,f(x) 函数图像的变化是递减 -> 递增 -> 递减,是一个反过来的 N 。
- 有界性
无界。
- 单调性
根据导数函数 f(x)' 函数的开口方向不同而不同。当开口向上时,单调性 递增 -> 递减 -> 递增,当开口向下时递减 -> 递增 -> 递减。
- 奇偶性
可能为奇函数,也可能非奇非偶。
- 周期性
无。
六. 对数函数 #
对数函数是形为 f(x) = loga(x)的函数,其中 a 为底数,必须满足 a > 0 并且 a != 1,定义域必须满足 x > 0。下面分别是底数大于1和小于1的对数函数图像。
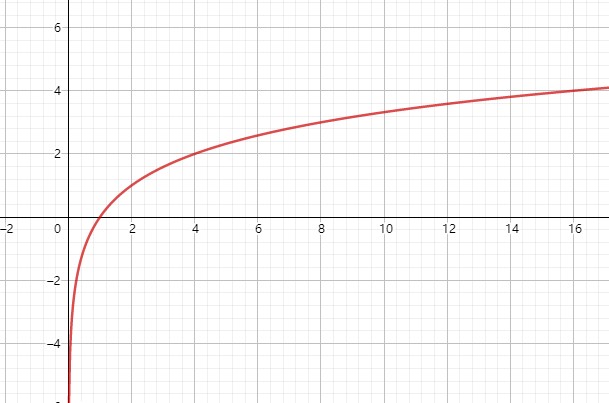
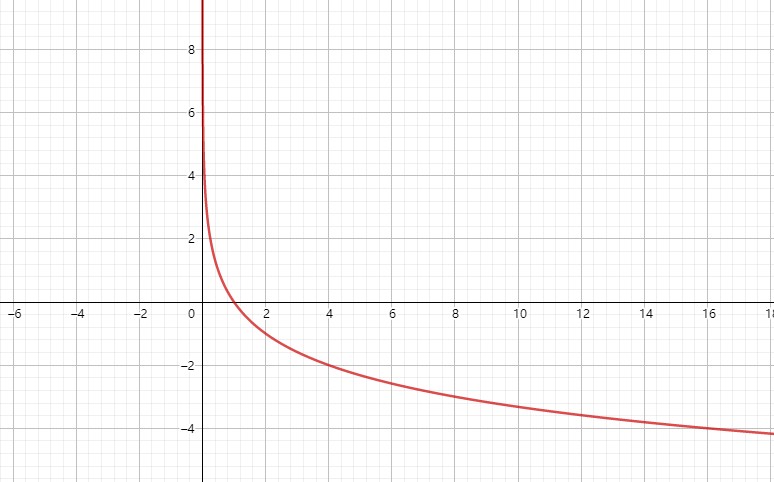
- 有界性
无界。
- 单调性
当底数 a > 1 时,递增,a < 1 时,递减。
- 奇偶性
非奇非偶。
- 周期性
无。
七. 指数函数 #
形为 f(x) = aˣ 的函数,称之为指数函数,其中 a 不等于1且大于0(等于1时,函数图像为 y = 1 的直线)。下图分别是当 a > 1 和 a < 1 时,指数函数的图像。
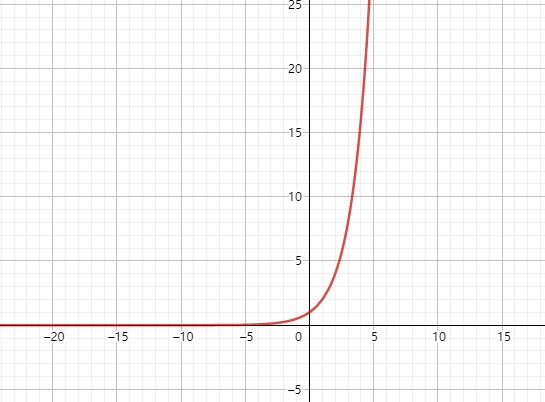
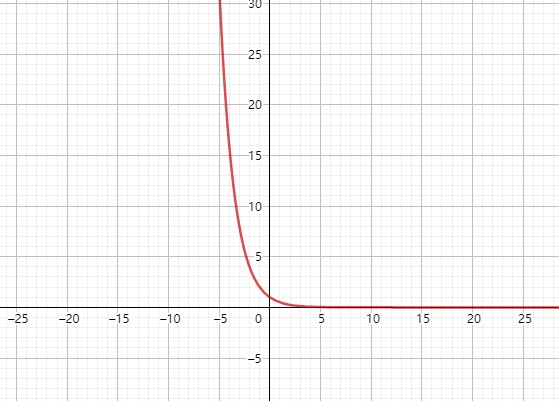
- 有界性
有下界,无上界。
- 单调性
当a > 1 时,递增,a < 1 时,递减。
- 奇偶性
非奇非偶。
- 周期性
无。
八. 正弦函数 #
正弦函数f(x) = sin(x)。
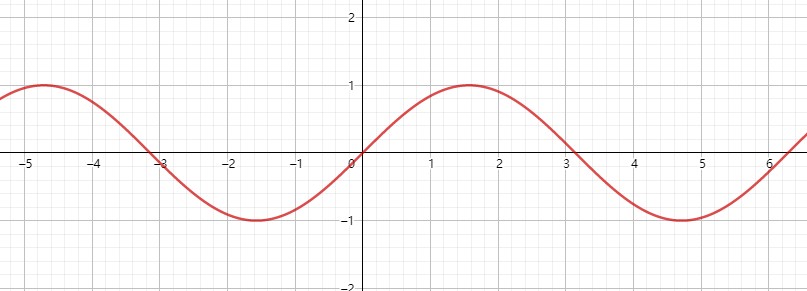
- 有界性
有上下界,上界为1,下界为-1。
- 单调性
在 x 属于 [2kπ - π / 2, 2kπ + π / 2]时递增,x 属于[2kπ + π / 2, 2kπ + 3π / 2]时递减,其中 k∈Z。
- 奇偶性
奇函数。
- 周期性
有周期性,周期为 2π。
九. 余弦函数 #
余弦函数f(x) = cos(x)。
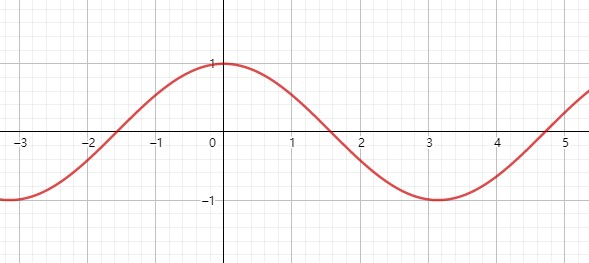
- 有界性
有上下界,上界为1,下界为-1。
- 单调性
在 x 属于 [2kπ - π, 2kπ]时递增,x 属于[2kπ, (2k + 1)π]时递减,其中 k∈Z。
- 奇偶性
偶函数。
- 周期性
有周期性,周期为 2π。
十. 正切函数 #
正切函数为f(x) = tan(x)。
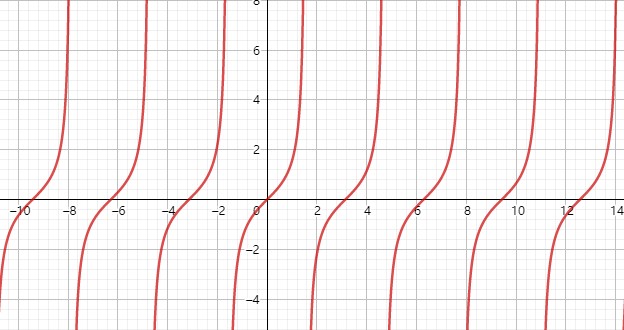
- 有界性
无界。
- 单调性
正切函数并非完全递增的,由图可知,它的单调递增区间为 (-π/2+kπ,+π/2+kπ), k∈Z。
- 奇偶性
奇函数。
- 周期性
有周期性,周期为 π。
(完)