埃尔米特曲线 #

通过拉格朗日插值和艾特肯插值并不能获得理想的曲线，因为经常会出现曲线越过节点的情况。

所以这里介绍另一种曲线：Hermite Curves，即埃尔米特曲线。

可以在这里查看埃尔米特曲线演示：https://www.geogebra.org/m/cs4dvwbh

埃尔米特曲线是一个三次曲线，三次曲线有四个系数，它由以下几个信息构建而来：

我们称起点和终点分别为 $p_0$ 和 $p_1$ ，速度分别为 $v_0$ 和 $v_1$ ，下图是一些埃尔米特曲线。

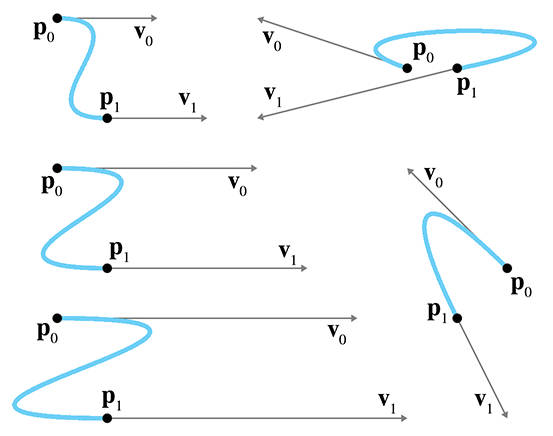
hermite curves

三次曲线方程为：

p(t) = c_0 + c_1t + c_2t^2 + c_3t^3

所以有以下等式成立:

\begin{aligned} p(0) = p_0 \qquad &=> \qquad c_0 = p_0 \\ v(0) = v_0 \qquad &=> \qquad c_1 = v_0 \\ v(1) = v_1 \qquad &=> \qquad c_1 + 2c_2 + 3c_3 = v_1 \\ p(1) = p_1 \qquad &=> \qquad c_0 + c_1 + c_2 + c_3 = p_1 \\ \end{aligned}

将上式转换为：

\begin{aligned} c_0 &= p_0 \\ c_1 &= v_0 \\ c_2 &= -3p_0 - 2v_0 - v_1 + 3p_1 \\ c_3 &= 2p_0 + v_0 + v_1 - 2p_1 \end{aligned}

可以将曲线的参数方程表示为矩阵形式：

p(t) = Ct = \begin{bmatrix} c_0 & c_1 & c_2 &c_3 \end{bmatrix} \begin{bmatrix} 1 \\ t \\ t^2 \\ t^3 \end{bmatrix}

注意 $c_i$ 是一个列向量，它的维数与几何维数有关（1D，2D 或者 3D）。

由 $c$ 与 $p_i$ 和速度 $v_i$ 的公式可以将上述矩阵转换为称如下的 PHt 格式：

p(t) = Ct = PHt = \begin{bmatrix} p_0 & v_0 & v_1 &p_1 \end{bmatrix} \begin{bmatrix} 1 & 0 & -3 & 2 \\ 0 & 1 & -2 & 1 \\ 0 & 0 & -1 & 1 \\ 0 & 0 & 3 & -2 \\ \end{bmatrix} \begin{bmatrix} 1 \\ t \\ t^2 \\ t^3 \end{bmatrix} \\ = p(Ht) = \begin{bmatrix} p_0 & v_0 & v_1 &p_1 \end{bmatrix} \begin{bmatrix} 1-3t^2 + 2t^3 \\ t - 2t^2 + t^3 \\ -t^2 + t^3 \\ 3t^2 - 2t^3 \end{bmatrix}

所以得到 $H_i(t)$ 为：

\begin{aligned} H_0(t) &= 1-3t^2 + 2t^3 \\ H_1(t) &= t - 2t^2 + t^3 \\ H_2(t) &= -t^2 + t^3 \\ H_3(t) &= 3t^2 - 2t^3 \end{aligned}

所以可以得到 p(t) 最终公式如下：

\begin{aligned} p(t) &= \begin{bmatrix} p_0 & v_0 & v_1 &p_1 \end{bmatrix} \begin{bmatrix} H_0(t) \\ H_1(t) \\ H_2(t) \\ H_3(t) \end{bmatrix} \\ &= H_0(t)p_0 + H_1(t)v_0 + H_2(t)v_1 + H_3(t)p_1 \end{aligned}

（完）