二叉树（binary tree）是指树中节点的度不大于2的有序树，它是一种最简单且最重要的树。二叉树的递归定义为：二叉树是一棵空树，或者是一棵由一个根节点和两棵互不相交的，分别称作根的左子树和右子树组成的非空树；左子树和右子树又同样都是二叉树。
一般涉及到树的算法都是比较困难的，而二叉树是一种最简单的也是最重要的树结构，所以面试的时候，面试官喜欢问一些关于二叉树的问题及算法。二叉树有三种遍历方式：前序遍历（先序遍历）、中序遍历、后序遍历。这几种遍历方式的名称是根据根节点的遍历次序命名的。
前序遍历（先序遍历）：先遍历根节点，在遍历左子节点，最后遍历右子节点。
中序遍历：先遍历左子节点，在遍历根节点，最后遍历右子节点。
后序遍历：先遍历左子节点，在遍历右节点，最后遍历根节点。
例如有如下的二叉树。
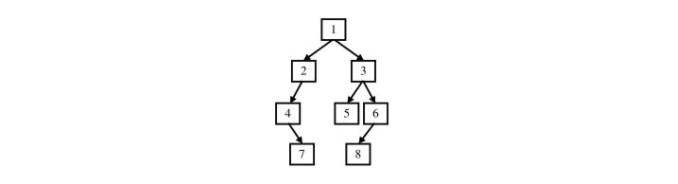
前序遍历：1,2,4,7,3,5,6,8。 中序遍历：4,7,2,1,5,3,8,6。 后序遍历：7,4,2,5,8,6,3,1。
题目：已知一颗二叉树的任意节点值都不重复，知道其前序遍历结果和中序遍历结果，求该二叉树。例如前序遍历结果为1,2,4,7,3,5,6,8，中序遍历结果为4,7,2,1,5,3,6,8。
通过上面二叉树的特性，我们知道前序遍历的遍历顺序为根->左->右，中序遍历的顺序为左->根->右。在前序遍历中我们可以得出1为根节点。那么又由中序遍历知道根节点的前面为左子树，后面为右子树，所以4,7,2为根节点的左子树的中序遍历，5,3,6,8为根节点的右子树的中序遍历。因为二叉树的值不重复，所以通过左子树的值，可以从该树的前序遍历结果中得到2,4,7为左子树的前序遍历，3,5,6,8为右子树的前序遍历。现在我们分别得到了左子树和右子树的前序遍历结果和中序遍历结果。只需要分别将左子树和右子树重复上面的步骤，就可以得到该二叉树。
interface TreeNode {
/**
* 当前值
*/
name: string;
/**
* 左子树和右子树，0为左子树，1为右子树
*/
children?: TreeNode[]
}
const getBinaryTree = (preTraversal: string[], midTraversal: string[]): TreeNode => {
if (preTraversal.length !== midTraversal.length) {
throw new Error("输入参数有误！");
}
if (preTraversal.length === 0) {
return {name: null};
}
if (preTraversal.length === 1) {
if (preTraversal[0] !== midTraversal[0]) {
throw new Error("输入参数有误！");
} else {
return {
name: preTraversal[0].toString()
}
}
}
const rootValue = preTraversal[0]; // 根节点
const rootIndex = midTraversal.indexOf(rootValue)
const leftMidTraverSal = midTraversal.slice(0, rootIndex); // 左子树的中序遍历
const rightMidTraversal = midTraversal.slice(rootIndex + 1); // 右子树的中序遍历
const leftPreTraversal: string[] = []; // 左子树的前序遍历
let rightPreTraversal: string[] = []; // 右子树的前序遍历
let i = 1;
for (; i < preTraversal.length; i++) {
const value = preTraversal[i];
if (leftMidTraverSal.indexOf(value) !== -1) {
leftPreTraversal.push(value);
} else {
break;
}
}
rightPreTraversal = preTraversal.slice(i);
const leftTree = getBinaryTree(leftPreTraversal, leftMidTraverSal);
const rightTree = getBinaryTree(rightPreTraversal, rightMidTraversal);
return {
name: rootValue.toString(),
children: [
leftTree,
rightTree
]
}
};
（完）